【题目】如图,矩形ABCD的顶点A、B的坐标分别为(-4,0)和(2,0),BC=![]() .设直线AC与直线x=4交于点E.
.设直线AC与直线x=4交于点E.
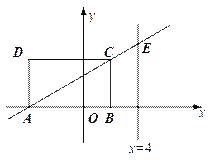
(1)求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E;
(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于C、N之间的一动点,求△CMN面积的最大值.
参考答案:
【答案】(1)略
(2)![]()
【解析】
解:(1)点C的坐标![]() .设抛物线的函数关系式为y=a(x–4)2+m,
.设抛物线的函数关系式为y=a(x–4)2+m,
则![]() ,解得
,解得![]()
∴所求抛物线的函数关系式为![]() …………①
…………①
设直线AC的函数关系式为![]() 则
则![]() ,解得
,解得![]() .
.
∴直线AC的函数关系式为![]() ,∴点E的坐标为
,∴点E的坐标为![]()
把x=4代入①式,得![]() ,∴此抛物线过E点.
,∴此抛物线过E点.
(2)(1)中抛物线与x轴的另一个交点为N(8,0),设M(x,y),
过M作MG⊥x轴于G,
则S△CMN=S△MNG+S梯形MGBC—S△CBN=![]()
=![]()
=![]()
∴当x=5时,S△CMN有最大值![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
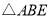 ,
,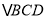 均为等边三角形,点
均为等边三角形,点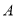 ,
,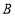 ,
,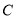 在同一条直线上,连接
在同一条直线上,连接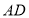 ,
,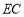 ,
,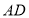 与
与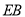 相交于点
相交于点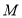 ,
,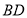 与
与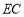 相交于点
相交于点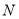 ,连接
,连接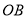 ,下列结论正确的有_________.
,下列结论正确的有_________.①
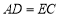 ;②
;②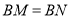 ;③
;③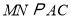 ;④
;④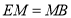 ;⑤
;⑤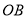 平分
平分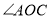
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
(3)点P(a+1,b-1)与点C关于x轴对称,则a= ,b= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
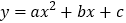 的图象开口向上,图象经过点
的图象开口向上,图象经过点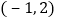 和
和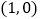 ,且与
,且与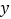 轴相交于负半轴.
轴相交于负半轴.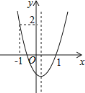
第
 问:给出四个结论:①
问:给出四个结论:① ;②
;② ;③
;③ ;④
;④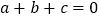 .写出其中正确结论的序号(答对得
.写出其中正确结论的序号(答对得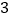 分,少选、错选均不得分)
分,少选、错选均不得分)第
 问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号.
问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在
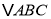 中,
中,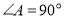 ,
,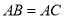 ,点
,点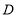 是斜边
是斜边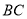 的中点,点
的中点,点 ,
,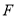 分别在线段
分别在线段 ,
,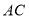 上, 且
上, 且 .
.(1)求证:
 为等腰直角三角形;
为等腰直角三角形;(2)若
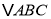 的面积为7,求四边形
的面积为7,求四边形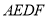 的面积;
的面积;(3)如图(2),如果点
 运动到
运动到 的延长线上时,点
的延长线上时,点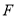 在射线
在射线 上且保持
上且保持 ,
, 还是等腰直角三角形吗.请说明理由.
还是等腰直角三角形吗.请说明理由. 

-
科目: 来源: 题型:
查看答案和解析>>【题目】课本中有一道作业题:
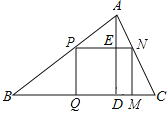
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
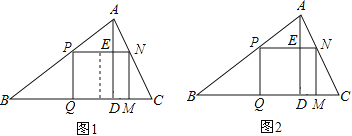
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在一个边长为1的小正方形组成的方格稿纸上,有A、B、C、D、E、F、G七个点,则在下列任选三个点的方案中可以构成直角三角形的是( )
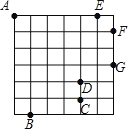
A.点A、点B、点CB.点A、点D、点G
C.点B、点E、点FD.点B、点G、点E
相关试题

