【题目】已知,AB//ED, BF平分∠ABC, DF平分∠EDC.
(1)若∠ABC =130°,∠EDC=110°,求∠C的度数和∠BFD的度数;
(2)请直接写出∠BFD与∠C的关系.

参考答案:
【答案】(1)![]()
![]()
![]()
![]()
【解析】
(1)过点C作CN//AB,过点F作FM//AB,根据平行线的性质得![]()
![]()
![]() 根据∠ABC =130°,∠EDC=110°,即可求出
根据∠ABC =130°,∠EDC=110°,即可求出
∠C的度数;根据角平分线的性质求出![]()
![]() 根据平行线的性质求出
根据平行线的性质求出![]()
![]() 即可求出∠BFD的度数;
即可求出∠BFD的度数;
(2)参照(1)的解题思路进行求解即可.
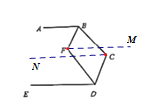
(1)如图,过点C作CN//AB,过点F作FM//AB.
![]() CN//AB,
CN//AB,
![]()
![]()
![]() AB//ED
AB//ED
![]() CN//ED
CN//ED
![]()
![]()
∠ABC =130°,∠EDC=110°,
![]()
![]()
![]() BF平分∠ABC, DF平分∠EDC,
BF平分∠ABC, DF平分∠EDC,
![]()
![]()
![]() FM//AB.
FM//AB.
![]()
![]() AB//ED.
AB//ED.
![]() FM//ED
FM//ED
![]()
![]()
∠BCD的度数和∠BFD的度数均为![]() ;
;
(2)![]()
理由如下:
![]() CN//AB,
CN//AB,
![]()
![]() AB//ED
AB//ED
![]() CN//ED
CN//ED
![]()
![]()
![]()
![]()
![]() BF平分∠ABC, DF平分∠EDC,
BF平分∠ABC, DF平分∠EDC,
![]()
![]()
![]() FM//AB.
FM//AB.
![]()
![]() AB//ED
AB//ED
![]() FM//ED,
FM//ED,
![]()
![]()
即![]()
![]()
∠BFD与∠BCD的关系为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车油箱内有油a升,从某地出发,每行驶1小时耗油6升,若设剩余油量为Q升,行驶时间为t/小时,根据以上信息回答下列问题:
(1)开始时,汽车的油量a=_____升;
(2)在_____小时汽车加油,加了_____升,
写出加油前Q与t之间的关系式______;
(3)这辆汽车行驶8小时,剩余油量多少升?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.
(1)如图(1),当点D在边BC上时,且n=36°,则∠BAD= _________,∠CDE= _________.
(2)如图(2),当点D运动到点B的左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由.
(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请画出图形,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.

(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠2,∠C=∠E, AE=AC,
(1)求证: △ABC≌△ADE;
(2) 求证:∠2=∠3;
(3)当∠2=90°时,判断△ABD的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.

(1)现随机转动转盘一次,停止后,指针指向1的概率是多少;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
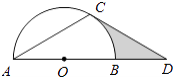
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
相关试题

