【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
(1)现随机转动转盘一次,停止后,指针指向1的概率是多少;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
参考答案:
【答案】
(1)解:根据题意得:随机转动转盘一次,停止后,指针指向1的概率为 ![]() ;
;
(2)解:列表得:
1 | 2 | 3 | |
1 | (1,1) | (2,1) | (3,1) |
2 | (1,2) | (2,2) | (3,2) |
3 | (1,3) | (2,3) | (3,3) |
所有等可能有9种,其中两数之积为偶数的情况有5种,之积为奇数的情况有5种,
因此P(小明获胜)=![]() ,P(小华获胜)=
,P(小华获胜)=![]()
∵![]() >
>![]()
∴游戏不公平。
【解析】(1)根据转盘上的数字可知,三个等可能情况中出现1的只有1种,利用概率公式即可求解。
(2)通过列表或画树状图的方法,分别求出两人获胜的概率,比较即可得出结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.

(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,AB//ED, BF平分∠ABC, DF平分∠EDC.
(1)若∠ABC =130°,∠EDC=110°,求∠C的度数和∠BFD的度数;
(2)请直接写出∠BFD与∠C的关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠2,∠C=∠E, AE=AC,
(1)求证: △ABC≌△ADE;
(2) 求证:∠2=∠3;
(3)当∠2=90°时,判断△ABD的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
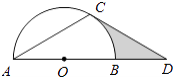
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图(1)).令△ABD不动,
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图(2)),证明:MB=MC.
(2)若将图(1)中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图(3)),判断MB、MC的数量关系,并说明理由.
(3)在(2)中,若∠CAE的大小改变(图(4)),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知射线AC是∠MAN的角平分线, ∠NAC=60°, B, D分别是射线AN. AM上的点,连接BD.
(1)在图①中,若∠ABC=∠ADC=90°,求∠CDB的大小;
(2)在图②中,若∠ABC+∠ADC=180°,求证:四边形ABCD的面积是个定值.
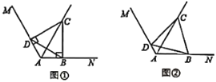
相关试题

