【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.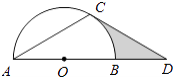
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
参考答案:
【答案】
(1)证明:连接OC. 
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠2=∠A=30°.
∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.即OC⊥CD,
∴CD是⊙O的切线.
(2)解:∵∠A=30°,
∴∠1=2∠A=60°.
∴S扇形BOC= ![]() .
.
在Rt△OCD中,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
∴ ![]() .
.
∴图中阴影部分的面积为: ![]()
![]() .
.
【解析】(1)要证CD是⊙O的切线,点C在半圆上,因此连接OC,需证明OC⊥CD。先根据等腰三角形的性质及三角形内角和定理求出∠2=∠A=∠D=30°.再求出∠OCD的度数,就可证出结论。
(2)根据图形分析阴影部分的面积=Rt△OCD的面积-扇形COB的面积,根据题意易求出∠1的度数,再利用解直角三角形求出CD的长,然后求出Rt△OCD的面积和扇形COB的面积,即可求得结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,AB//ED, BF平分∠ABC, DF平分∠EDC.
(1)若∠ABC =130°,∠EDC=110°,求∠C的度数和∠BFD的度数;
(2)请直接写出∠BFD与∠C的关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠2,∠C=∠E, AE=AC,
(1)求证: △ABC≌△ADE;
(2) 求证:∠2=∠3;
(3)当∠2=90°时,判断△ABD的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.

(1)现随机转动转盘一次,停止后,指针指向1的概率是多少;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图(1)).令△ABD不动,
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图(2)),证明:MB=MC.
(2)若将图(1)中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图(3)),判断MB、MC的数量关系,并说明理由.
(3)在(2)中,若∠CAE的大小改变(图(4)),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知射线AC是∠MAN的角平分线, ∠NAC=60°, B, D分别是射线AN. AM上的点,连接BD.
(1)在图①中,若∠ABC=∠ADC=90°,求∠CDB的大小;
(2)在图②中,若∠ABC+∠ADC=180°,求证:四边形ABCD的面积是个定值.
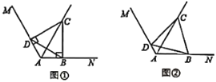
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格调查,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
相关试题

