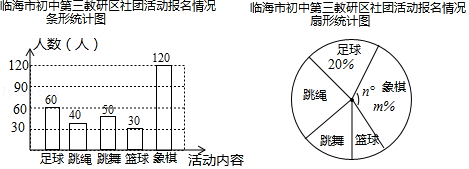
【题目】临海市初中第三教研区为了丰富学生课余活动,组织同学开展每周一次的社团活动,活动内容有足球、跳绳、跳舞、篮球、象棋共5项,为方便组织,规定每位同学只能报一项活动,根据报名绘制了如下两幅尚不完整的统计图,解答下列问题: 
(1)将条形统计图补充完整;
(2)写出扇形统计图中的m和n的值;
(3)瑶瑶和欣欣两名同学对足球、篮球、象棋三项活动都很感兴趣,决定从三项活动中随机抽取一项参加,利用树状图或列表表示所有可能结果,并求出两人参加同一项目的概率;
(4)由于场地限制,参加足球活动的学生人数不能超过参加其余活动学生人数的 ![]() ,那么至少几位同学需要从参加足球活动调整到参加其余活动?
,那么至少几位同学需要从参加足球活动调整到参加其余活动?
参考答案:
【答案】
(1)解:本次调查的学生总数为60÷20%=300(人),
∴选择“跳绳”的学生有300﹣(60+50+30+120)=40(人),
补全图形为:
(2)解:扇形统计图中象棋所占百分比为m%= ![]() ×100%=40%,其圆心角度数为360°×40%=144°,
×100%=40%,其圆心角度数为360°×40%=144°,
∴m=40,n=144;
(3)解:设足球、篮球、象棋三项活动分别为A,B,C,
画树状图得:
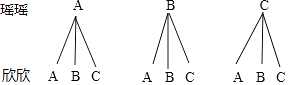
∴所求概率P(同一项活动)= ![]() =
= ![]() ;
;
(4)解:设x位同学从参加足球项目调整到其他项目.
根据题意,得:60﹣x≤ ![]() (240+x),
(240+x),
解得:x≥17 ![]() ,
,
∵x为整数,
∴至少需要18位学生调离足球
【解析】(1)由足球人数及其百分比求得总人数,再减去其余活动人数可得跳绳人数,即可补全条形图;(2)用象棋人数除以总人数可得百分比,再乘以360度可得n的值;(3)画树状图列出所有等可能结果,再找到同一活动的结果数,根据概率公式可得答案;(4)设x位同学从参加足球项目调整到其他项目,根据“参加足球活动的学生人数不能超过参加其余活动学生人数的 ![]() ”列不等式求解可得.
”列不等式求解可得.
【考点精析】根据题目的已知条件,利用扇形统计图和条形统计图的相关知识可以得到问题的答案,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设
 ,
,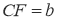 ,满足
,满足 .
.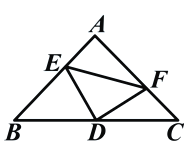
(1)求BE及CF的长。
(2)求证:
 。
。(3)在(1)的条件下,求△DEF的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,点P的坐标为(m+1,m-1).

(1)试判断点P是否在一次函数y=x-2的图象上,并说明理由;
(2)如图,一次函数y=-
 x+3的图象与x轴、y轴分别相交于A,B,若点P在△AOB的内部,求m的取值范围.
x+3的图象与x轴、y轴分别相交于A,B,若点P在△AOB的内部,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD是两个过江电缆的铁塔,塔AB高40米,AB的中点为P,塔底B距江面的垂直高度为6米.跨江电缆因重力自然下垂近似成抛物线形,为了保证过往船只的安全,电缆下垂的最低点距江面的高度不得少于30米.已知:人在距塔底B点西50米的地面E点恰好看到点E、P、C在一直线上;再向西前进150米后从地面F点恰好看到点F、A、C在一直线上.
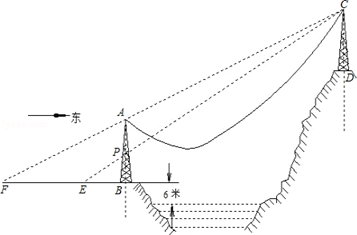
(1)求两铁塔轴线间的距离(即直线AB、CD间的距离);
(2)若以点A为坐标原点,向东的水平方向为x轴,取单位长度为1米,BA的延长方向为y轴建立坐标系.求刚好满足最低高度要求的这个抛物线的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨
 元收费
元收费 如果超过20吨,未超过的部分按每吨
如果超过20吨,未超过的部分按每吨 元收费,超过的部分按每吨
元收费,超过的部分按每吨 元收费
元收费 设某户每月用水量为x吨,应收水费为y元.
设某户每月用水量为x吨,应收水费为y元. 设某户居民每月用水量为m吨
设某户居民每月用水量为m吨 ,则应收水费为______元
,则应收水费为______元 用含m的代数式表示
用含m的代数式表示 ;
; 设某户居民每月用水量为m吨
设某户居民每月用水量为m吨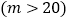 ,则应收水费为______元
,则应收水费为______元 用含m的代数式表示
用含m的代数式表示 ;
; 若该城市某户5月份水费平均为每吨
若该城市某户5月份水费平均为每吨 元,求该户5月份用水多少吨?
元,求该户5月份用水多少吨? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2 h,并且甲车途中休息了0.5 h,如图是甲、乙两车行驶的路程y(km)与时间x(h)的函数图象.
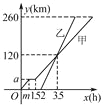
(1)求出图中m和a的值.
(2)求出甲车行驶的路程y(km)与时间x(h)的函数关系式,并写出相应的x的取值范围.
(3)当乙车行驶多长时间时,两车恰好相距50 km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=130°,射线OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的角平分线,下列叙述正确的是( )
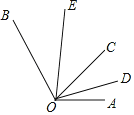
A. ∠DOE的度数不能确定 B. ∠AOD=
 ∠EOC
∠EOCC. ∠AOD+∠BOE=65° D. ∠BOE=2∠COD
相关试题

