【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设![]() ,
,![]() ,满足
,满足![]() .
.
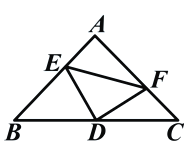
(1)求BE及CF的长。
(2)求证:![]() 。
。
(3)在(1)的条件下,求△DEF的面积。
参考答案:
【答案】(1)BE=12,CF=5;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)先根据二次根式的非负性求出m=2,再由非负数的性质求出a、b的值,进而得到BE及CF的长;
(2)延长ED到P,使DP=DE,连接FP,CP,利用SAS得到三角形BED与三角形CPD全等,利用全等三角形对应边相等得到BE=CP,再利用SAS得到△EDF和△PDF全等,利用全等三角形对应边相等得到EF=FP,利用等角的余角相等得到∠FCP为直角,在直角三角形FCP中,利用勾股定理列出关系式,等量代换即可得证;
(3)连接AD,由AB=AC,且D为BC的中点,利用三线合一得到AD垂直于BC,AD为角平分线,再由三角形ABC为等腰直角三角形,得到一对角相等,利用同角的余角相等得到一对角相等,再由AD=CD,利用ASA得到三角形AED与三角形CFD全等,利用全等三角形对应边相等得到AE=CF=5,DE=DF,由AE+EB求出AB的长,即为AC的长,再由AC-CF求出AF的长,在直角三角形AEF中,利用勾股定理求出EF的长,再根据三角形DEF为等腰直角三角形求出DE与DF的长,即可确定出三角形DEF的面积.
试题解析:(1)由题意得![]() ,
,
解得m=2,
则![]() +|b-5|=0,
+|b-5|=0,
所以a-12=0,b-5=0,
a=12,b=5,
即BE=12,CF=5;
(2)延长ED到P,使DP=DE,连接FP,CP,

在△BED和△CPD中,
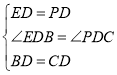 ,
,
∴△BED≌△CPD(SAS),
∴BE=CP,∠B=∠CDP,
在△EDF和△PDF中,
 ,
,
∴△EDF≌△PDF(SAS),
∴EF=FP,
∵∠B=∠DCP,∠A=90°,
∴∠B+∠ACB=90°,
∴∠ACB+∠DCP=90°,即∠FCP=90°,
在Rt△FCP中,根据勾股定理得:CF2+CP2=PF2,
∵BE=CP,PF=EF,
∴BE2+CF2=EF2;
(3)连接AD,
∵△ABC为等腰直角三角形,D为BC的中点,
∴∠BAD=∠FCD=45°,AD=BD=CD,AD⊥BC,
∵ED⊥FD,
∴∠EDA+∠ADF=90°,∠ADF+∠FDC=90°,
∴∠EDA=∠FDC,
在△AED和△CFD中,
 ,
,
∴△AED≌△CFD(ASA),
∴AE=CF=5,DE=DF,即△EDF为等腰直角三角形,
∴AB=AE+EB=5+12=17,
∴AF=AC-FC=AB-CF=17-5=12,
在Rt△EAF中,根据勾股定理得:EF=![]() =13,
=13,
设DE=DF=x,
根据勾股定理得:x2+x2=132,
解得:x=![]() ,即DE=DF=
,即DE=DF=![]() ,
,
则S△DEF=![]() DEDF=
DEDF=![]() ×
×![]() ×
×![]() =
=![]() .
.
-
科目: 来源: 题型:
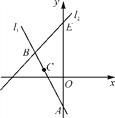
查看答案和解析>>【题目】如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.
(1)求点C的坐标和直线l1的解析式;
(2)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上A 点对应的数为﹣5,B 点在A 点右边,电子蚂蚁甲、乙在B分别以2个单位/秒、1个单位/秒的速度向左运动,电子蚂蚁丙在A 以3个单位/秒的速度向右运动.
(1)若电子蚂蚁丙经过5秒运动到C 点,求C 点表示的数;

(2)若它们同时出发,若丙在遇到甲后1秒遇到乙,求B 点表示的数;

(3)在(2)的条件下,设它们同时出发的时间为t 秒,是否存在t的值,使丙到乙的距离是丙到甲的距离的2倍?若存在,求出t 值;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.
如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若(
 ☆3)☆(﹣
☆3)☆(﹣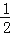 )=8,求a的值;
)=8,求a的值;(3)若2☆x=m,(
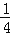 x)☆3=n(其中x为有理数),试比较m,n的大小.
x)☆3=n(其中x为有理数),试比较m,n的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,点P的坐标为(m+1,m-1).

(1)试判断点P是否在一次函数y=x-2的图象上,并说明理由;
(2)如图,一次函数y=-
 x+3的图象与x轴、y轴分别相交于A,B,若点P在△AOB的内部,求m的取值范围.
x+3的图象与x轴、y轴分别相交于A,B,若点P在△AOB的内部,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD是两个过江电缆的铁塔,塔AB高40米,AB的中点为P,塔底B距江面的垂直高度为6米.跨江电缆因重力自然下垂近似成抛物线形,为了保证过往船只的安全,电缆下垂的最低点距江面的高度不得少于30米.已知:人在距塔底B点西50米的地面E点恰好看到点E、P、C在一直线上;再向西前进150米后从地面F点恰好看到点F、A、C在一直线上.
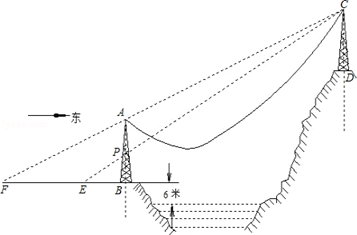
(1)求两铁塔轴线间的距离(即直线AB、CD间的距离);
(2)若以点A为坐标原点,向东的水平方向为x轴,取单位长度为1米,BA的延长方向为y轴建立坐标系.求刚好满足最低高度要求的这个抛物线的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】临海市初中第三教研区为了丰富学生课余活动,组织同学开展每周一次的社团活动,活动内容有足球、跳绳、跳舞、篮球、象棋共5项,为方便组织,规定每位同学只能报一项活动,根据报名绘制了如下两幅尚不完整的统计图,解答下列问题:

(1)将条形统计图补充完整;
(2)写出扇形统计图中的m和n的值;
(3)瑶瑶和欣欣两名同学对足球、篮球、象棋三项活动都很感兴趣,决定从三项活动中随机抽取一项参加,利用树状图或列表表示所有可能结果,并求出两人参加同一项目的概率;
(4)由于场地限制,参加足球活动的学生人数不能超过参加其余活动学生人数的 ,那么至少几位同学需要从参加足球活动调整到参加其余活动?
,那么至少几位同学需要从参加足球活动调整到参加其余活动?
相关试题

