【题目】如图,AB、CD是两个过江电缆的铁塔,塔AB高40米,AB的中点为P,塔底B距江面的垂直高度为6米.跨江电缆因重力自然下垂近似成抛物线形,为了保证过往船只的安全,电缆下垂的最低点距江面的高度不得少于30米.已知:人在距塔底B点西50米的地面E点恰好看到点E、P、C在一直线上;再向西前进150米后从地面F点恰好看到点F、A、C在一直线上.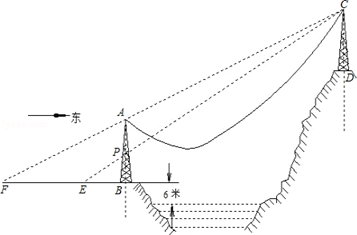
(1)求两铁塔轴线间的距离(即直线AB、CD间的距离);
(2)若以点A为坐标原点,向东的水平方向为x轴,取单位长度为1米,BA的延长方向为y轴建立坐标系.求刚好满足最低高度要求的这个抛物线的解析式.
参考答案:
【答案】
(1)
解:如图,AB=40米,BP=20米,BE=50米,BF=50+150=200(米).
设CD的延长线交地平面于点H.
设CH=x,BH=y
由△EBP∽△EHC得 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ①
①
由△FBA∽△FHC得 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ②
②
由①②解得:x=60,y=100
答:两铁塔轴线间的距离为100米;
(2)
解:依题意建立坐标系如图,由(1)得CH=60米,C点比A点高20米,
这时A、C两点的坐标为:A(0,0),C(100,20),
设抛物线顶点为P(x0,y0),
因为要求最低点高于地面为30﹣6=24(米),点A高度为40米,所以y0=﹣16.
设过点A的抛物线解析式为y=ax2+bx(a>0),则该抛物线满足:

化简得:125b2+80b﹣16=0
解得:b1= ![]() ,b2=﹣
,b2=﹣ ![]()
∵抛物线的对称轴在y轴的右侧,有 ![]() >0,而a>0
>0,而a>0
∴b<0,故b1= ![]() 舍去
舍去
把b2=﹣ ![]() 代入前式得:a=
代入前式得:a= ![]()
∴y= ![]() x2﹣
x2﹣ ![]() x
x
答:所求抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x.
x.

【解析】(1)根据题意,连接CA并延长到F,连接CP并延长到E,CD的延长线交地平面于点H.于是构造了两对相似三角形:EBP∽△EHC,△FBA∽△FHC,利用相似三角形的性质,建立起AB、CD之间的关系式,解方程组即可;(2)因为点A为坐标原点,则可设过原点的二次函数解析式为y=ax2+bx(a>0),将C(100,20)代入上式可得关于a、b的关系式,再根据二次函数顶点坐标公式和最低点高于地面为30﹣6=24(米),点A高度为40米,得到关于a、b的关系式,于是可以求出二次函数解析式.
【考点精析】通过灵活运用关于坡度坡角问题,掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.
如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若(
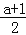 ☆3)☆(﹣
☆3)☆(﹣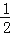 )=8,求a的值;
)=8,求a的值;(3)若2☆x=m,(
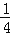 x)☆3=n(其中x为有理数),试比较m,n的大小.
x)☆3=n(其中x为有理数),试比较m,n的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设
 ,
,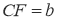 ,满足
,满足 .
.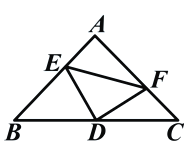
(1)求BE及CF的长。
(2)求证:
 。
。(3)在(1)的条件下,求△DEF的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,点P的坐标为(m+1,m-1).

(1)试判断点P是否在一次函数y=x-2的图象上,并说明理由;
(2)如图,一次函数y=-
 x+3的图象与x轴、y轴分别相交于A,B,若点P在△AOB的内部,求m的取值范围.
x+3的图象与x轴、y轴分别相交于A,B,若点P在△AOB的内部,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】临海市初中第三教研区为了丰富学生课余活动,组织同学开展每周一次的社团活动,活动内容有足球、跳绳、跳舞、篮球、象棋共5项,为方便组织,规定每位同学只能报一项活动,根据报名绘制了如下两幅尚不完整的统计图,解答下列问题:

(1)将条形统计图补充完整;
(2)写出扇形统计图中的m和n的值;
(3)瑶瑶和欣欣两名同学对足球、篮球、象棋三项活动都很感兴趣,决定从三项活动中随机抽取一项参加,利用树状图或列表表示所有可能结果,并求出两人参加同一项目的概率;
(4)由于场地限制,参加足球活动的学生人数不能超过参加其余活动学生人数的 ,那么至少几位同学需要从参加足球活动调整到参加其余活动?
,那么至少几位同学需要从参加足球活动调整到参加其余活动? -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨
 元收费
元收费 如果超过20吨,未超过的部分按每吨
如果超过20吨,未超过的部分按每吨 元收费,超过的部分按每吨
元收费,超过的部分按每吨 元收费
元收费 设某户每月用水量为x吨,应收水费为y元.
设某户每月用水量为x吨,应收水费为y元. 设某户居民每月用水量为m吨
设某户居民每月用水量为m吨 ,则应收水费为______元
,则应收水费为______元 用含m的代数式表示
用含m的代数式表示 ;
; 设某户居民每月用水量为m吨
设某户居民每月用水量为m吨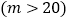 ,则应收水费为______元
,则应收水费为______元 用含m的代数式表示
用含m的代数式表示 ;
; 若该城市某户5月份水费平均为每吨
若该城市某户5月份水费平均为每吨 元,求该户5月份用水多少吨?
元,求该户5月份用水多少吨? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2 h,并且甲车途中休息了0.5 h,如图是甲、乙两车行驶的路程y(km)与时间x(h)的函数图象.
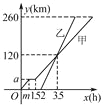
(1)求出图中m和a的值.
(2)求出甲车行驶的路程y(km)与时间x(h)的函数关系式,并写出相应的x的取值范围.
(3)当乙车行驶多长时间时,两车恰好相距50 km?
相关试题

