【题目】如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.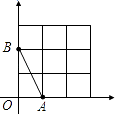
(1)求线段AB所在直线的函数解析式,并写出当0≤y≤2时,自变量x的取值范围;
(2)将线段AB绕点B逆时针旋转90°,得到线段BC,请在答题卡指定位置画出线段BC.若直线BC的函数解析式为y=kx+b,则y随x的增大而(填“增大”或“减小”).
参考答案:
【答案】
(1)
解:设直线AB的函数 解析式为y=kx+b(k、b为常数且k≠0)
依题意,得A(1,0),B(0,2)
∴ ![]()
解得 ![]()
∴直线AB的函数解析式为y=﹣2x+2
当0≤y≤2时,自变量x的取值范围是0≤x≤1
(2)
解:线段BC即为所求.
故答案为:增大
【解析】(1)根据一次函数图象知A(1,0),B(0,2),然后将其代入一次函数的解析式,利用待定系数法求该函数的解析式;(2)根据旋转的性质,在答题卡中画出线段BC,然后根据直线BC的单调性填空.
【考点精析】关于本题考查的确定一次函数的表达式,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.

(1)求DE的长;
(2)求△ADB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
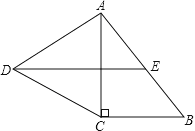
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】城区某中学为形成体育特色,落实学生每天
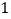 小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.
小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.国家规定初中每班的标准人数为
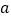 人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的
人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的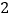 倍少
倍少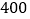 人,九年级学生人数的
人,九年级学生人数的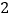 倍刚好是七、八年级学生人数的总和.(注:
倍刚好是七、八年级学生人数的总和.(注: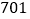 班表示七年级一班)
班表示七年级一班)班级
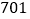 班
班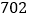 班
班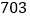 班
班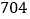 班
班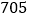 班
班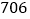 班
班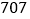 班
班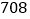 班
班和每班标准
人数的差值
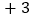
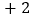
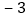
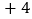
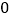
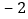
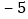
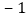
 用含
用含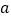 的式子表示该中学七年级学生总数;
的式子表示该中学七年级学生总数; 学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根
学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根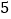 元,毽球每个
元,毽球每个 元,羽毛球拍每副
元,羽毛球拍每副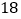 元.请你计算当
元.请你计算当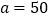 时,学校为落实
时,学校为落实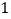 小时体育锻炼时间需购买器材的费用是多少?
小时体育锻炼时间需购买器材的费用是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.

求:
(1)tanC;
(2)图中两部分阴影面积的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中, ①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面一段:
计算
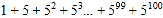
观察发现,上式从第二项起,每项都是它前面一项的
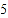 倍,如果将上式各项都乘以
倍,如果将上式各项都乘以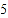 ,所得新算式中除个别项外,其余与原式中的项相同,于是两式相减将使差易于计算.
,所得新算式中除个别项外,其余与原式中的项相同,于是两式相减将使差易于计算.解:设
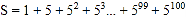 ,①
,①则
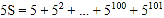 ,②
,②②-①得
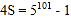 ,则
,则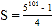 .
.上面计算用的方法称为“错位相减法”,如果一列数,从第二项起每一项与前一项之比都相等(本例中是都等于
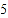 ),那么这列数的求和问题,均可用上述“错位相减”法来解决.
),那么这列数的求和问题,均可用上述“错位相减”法来解决.下面请你观察算式
 是否具备上述规律?若是,请你尝试用“错位相减”法计算上式的结果.
是否具备上述规律?若是,请你尝试用“错位相减”法计算上式的结果.
相关试题

