【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
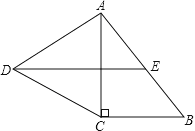
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
参考答案:
【答案】(1)首先连接CE,根据直角三角形的性质可得CE=![]() AB=AE,再根据等边三角形的性质可得AD=CD,然后证明△ADE≌△CDE,进而得到∠ADE=∠CDE=30°,再有∠DCB=150°可证明DE∥CB。
AB=AE,再根据等边三角形的性质可得AD=CD,然后证明△ADE≌△CDE,进而得到∠ADE=∠CDE=30°,再有∠DCB=150°可证明DE∥CB。
(2)当![]() 或AB=2AC时,四边形DCBE是平行四边形。
或AB=2AC时,四边形DCBE是平行四边形。
【解析】分析:(1)首先连接CE,根据直角三角形的性质可得CE=![]() AB=AE,再根据等边三角形的性质可得AD=CD,然后证明△ADE≌△CDE,进而得到∠ADE=∠CDE=30°,再有∠DCB=150°可证明DE∥CB。
AB=AE,再根据等边三角形的性质可得AD=CD,然后证明△ADE≌△CDE,进而得到∠ADE=∠CDE=30°,再有∠DCB=150°可证明DE∥CB。
(2)当![]() 或AB=2AC时,四边形DCBE是平行四边形。若四边形DCBE是平行四边形,则DC∥BE,∠DCB+∠B=180°进而得到∠B=30°,再根据三角函数可推出
或AB=2AC时,四边形DCBE是平行四边形。若四边形DCBE是平行四边形,则DC∥BE,∠DCB+∠B=180°进而得到∠B=30°,再根据三角函数可推出![]() 或AB=2AC。
或AB=2AC。
解:(1)证明:连结CE,
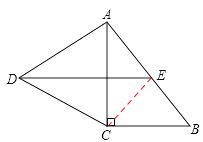
∵点E为Rt△ACB的斜边AB的中点,
∴CE=![]() AB=AE。
AB=AE。
∵△ACD是等边三角形,∴AD=CD。
在△ADE与△CDE中,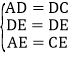 ,
,
∴△ADE≌△CDE(SSS)。∴∠ADE=∠CDE=30°。
∵∠DCB=150°,∴∠EDC+∠DCB=180°。
∴DE∥CB。
(2)∵∠DCB=150°,若四边形DCBE是平行四边形,则DC∥BE,∠DCB+∠B=180°。
∴∠B=30°.
在Rt△ACB中,sinB=![]() ,即sin30°=
,即sin30°=![]() ,∴
,∴![]() 或AB=2AC。
或AB=2AC。
∴当![]() 或AB=2AC时,四边形DCBE是平行四边形。
或AB=2AC时,四边形DCBE是平行四边形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读求绝对值不等式|x|<3和|x|>3的解集的过程:
因为|x|<3,从如图1所示的数轴上看:大于-3而小于3的数的绝对值是小于3的,所以|x|<3的解集是-3<x<3;
因为|x|>3,从如图2所示的数轴上看:小大于-3的数和大于3的数的绝对值是大于3的,所以|x|>3的解集是x<-3或x>3.
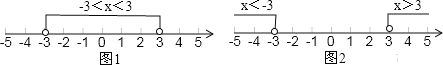
解答下面的问题:
(1)不等式|x|<a(a>0)的解集为______;不等式|x|>a(a>0)的解集为______.
(2)解不等式|x-5|<3;
(3)解不等式|x-3|>5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.

(1)求DE的长;
(2)求△ADB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】城区某中学为形成体育特色,落实学生每天
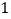 小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.
小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.国家规定初中每班的标准人数为
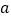 人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的
人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的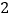 倍少
倍少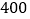 人,九年级学生人数的
人,九年级学生人数的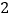 倍刚好是七、八年级学生人数的总和.(注:
倍刚好是七、八年级学生人数的总和.(注: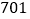 班表示七年级一班)
班表示七年级一班)班级
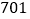 班
班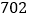 班
班 班
班 班
班 班
班 班
班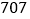 班
班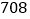 班
班和每班标准
人数的差值
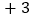
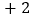
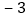
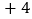
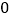
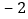
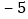
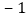
 用含
用含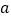 的式子表示该中学七年级学生总数;
的式子表示该中学七年级学生总数; 学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根
学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根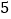 元,毽球每个
元,毽球每个 元,羽毛球拍每副
元,羽毛球拍每副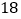 元.请你计算当
元.请你计算当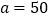 时,学校为落实
时,学校为落实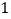 小时体育锻炼时间需购买器材的费用是多少?
小时体育锻炼时间需购买器材的费用是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
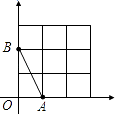
(1)求线段AB所在直线的函数解析式,并写出当0≤y≤2时,自变量x的取值范围;
(2)将线段AB绕点B逆时针旋转90°,得到线段BC,请在答题卡指定位置画出线段BC.若直线BC的函数解析式为y=kx+b,则y随x的增大而(填“增大”或“减小”). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.

求:
(1)tanC;
(2)图中两部分阴影面积的和.
相关试题

