【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形称为“中垂三角形”.设BC=a,AC=b,AB=c.
(特例探究)
(1)如图1,当tan∠PAB=1,c=2![]() 时,a= ,b= ;
时,a= ,b= ;
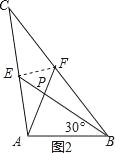
如图2,当∠PAB=30°,c=4时,a= ,b= ;
(归纳证明)
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(拓展证明)
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=6![]() ,AB=6,求AF的长.
,AB=6,求AF的长.

参考答案:
【答案】(1)4![]() ,4
,4![]() ,
,![]() ,
,![]() ;(2)猜想:a 2,b2,c2三者之间的关系是:a2+b2=5c2(3)AF=2
;(2)猜想:a 2,b2,c2三者之间的关系是:a2+b2=5c2(3)AF=2![]()
【解析】
试题(1)①由等腰直角三角形的性质得到AP=BP=![]() AB=4,根据三角形中位线的性质,得到EF∥AB,EF=
AB=4,根据三角形中位线的性质,得到EF∥AB,EF=![]() AB=2
AB=2![]() ,再由勾股定理得到结果;②如图2,连接EF,类比①,结合△PEF~△ABP进行求解;
,再由勾股定理得到结果;②如图2,连接EF,类比①,结合△PEF~△ABP进行求解;
(2)连接EF,类比着(1)即可证得结论;
(3)根据全等三角形的性质得到AG=GF,得到BG是△ABF的中线,取AB的中点H,连接FH,并延长交DA的延长线于P,推出四边形CSPF是平行四边形,根据平行四边形的性质得到FP∥CE,得到△ABF是中垂三角形,于是得到结论.
解:(1)∵AF⊥BE,∠ABE=45°,
∴AP=BP=![]() AB=4,
AB=4,
∵AF,BE是△ABC的中线,
∴EF∥AB,EF=![]() AB=2
AB=2![]() ,
,
∴∠PFE=∠PEF=45°,
∴PE=PF=2,
在Rt△FPB和Rt△PEA中,
AE=BF=![]() =2
=2![]() ,
,
∴AC=BC=4![]() ,
,
∴a=b=4![]() ,
,
如图2,连接EF,
同理可得:EF=![]() ×2=1,
×2=1,
∵EF∥AB,
∴△PEF~△ABP,
∴![]() =
=![]() ,
,
在Rt△ABP中,
AB=2,∠ABP=30°,
∴AP=1,PB=![]() ,
,
∴PF=![]() ,PE=
,PE=![]() ,
,
在Rt△APE和Rt△BPF中,
AE=![]() ,BF=
,BF=![]() ,
,
∴a=![]() ,b=
,b=![]() ,
,
故答案为:4![]() ,4
,4![]() ,
,![]() ,
,![]() ;
;
(2)猜想:a 2,b2,c2三者之间的关系是:a2+b2=5c2,
证明:如图3,连接EF,

∵AF,BE是△ABC的中线,
∴EF是△ABC的中位线,
∴EF∥AB.且 EF=![]() AB=
AB=![]() c.
c.
∴![]() =
=![]() =
=![]() ,
,
设 PF=m,PE=n 则AP=2m,PB=2n,
在Rt△APB中,(2m)2+(2n)2=c2①
在Rt△APE中,(2m)2+n2=(![]() )2②
)2②
在Rt△BPF中,m2+(2n)2=(![]() )2③
)2③
由①得:m2+n2=![]() ,由②+③得:5( m2+n2)=
,由②+③得:5( m2+n2)=![]() ,
,
∴a 2+b2=5 c2;
(3)在△AGE与△FGB中,
 ,
,
∴△AGE≌△FGB,
∴BG=EG,AG=GF,
∴BG是△ABF的中线,
如图4,取AB的中点H,连接FH,并延长交DA的延长线于P,

同理,△APH≌△BFH,
∴AP=BF,PE=CF=2BF,
∴PE∥CF,PE=CF,
∴四边形CSPF是平行四边形,
∴FP∥CE,
∵BE⊥CE,
∴FP⊥BE,即FH⊥BG,
∴△ABF是中垂三角形,
由(2)知,AB2+AF2=5BF2,
∵AB=6,BF=![]() AD=2
AD=2![]() ,
,
∴36+AF2=5×(2![]() )2,
)2,
∴AF=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A坐标(0,6),AC⊥y轴,且AC=AO,点B,C横坐标相同,点D在AC上,tan∠AOD=
 ,若反比例函数y=
,若反比例函数y= (x>0)的图象经过点B、D.
(x>0)的图象经过点B、D.(1)求:k及点B坐标;
(2)将△AOD沿着OD折叠,设顶点A的对称点A1的坐标是A1(m,n),求:代数式m+3n的值以及点A1的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB分别与两坐标轴交于点A(6,0),B(0,12),点C的坐标为(3,0)
(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为16,求点P的坐标.
②连结CP,是否存在点P,使△ACP与△AOB相似?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
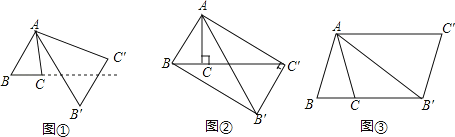
查看答案和解析>>【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
(1)如图①,对△ABC作变换[60°,
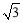 ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
-
科目: 来源: 题型:
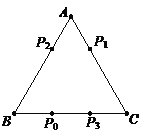
查看答案和解析>>【题目】电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=5.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1= CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2= AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3= BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2016与点P2017之间的距离为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点 A,B的坐标分别为(0,3),(1,0),△ABC是等腰直角三角形,∠ABC=90°.
(1)图1中,点C的坐标为 ;
(2)如图2,点D的坐标为(0,1),点E在射线CD上,过点B 作BF⊥BE交y轴于点F.
①当点E为线段CD的中点时,求点F的坐标;
②当点E在第二象限时,请直接写出F点纵坐标y的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为 ( )

A.8B.10C.12D.14
相关试题

