搜索
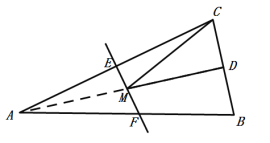
【题目】如图,等腰三角形ABC的底边BC为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为 （ ）
A.8B.10C.12D.14
参考答案：
【答案】D
【解析】
连接AD，根据等腰三角形的性质以及垂直平分线的性质结合三角形的面积公式求出AD的长，再根据垂直平分线的性质知点C关于直线EF的对称点为点A，故A、M、D共线时△CDM的周长的最小，由此即可得出结论．
连接AD，
∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，
∴
，
解得AD=12，
∵EF是线段AC的垂直平分线，
∴点C关于直线EF的对称点为点A，
∴AD的长为CM+MD的最小值，
∴△CDM的周长最短
故选：D
-
科目： 来源： 题型：
查看答案和解析>>【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AF、BE是△ABC的中线，AF⊥BE于点P，像△ABC这样的三角形称为“中垂三角形”．设BC=a，AC=b，AB=c．
（特例探究）
（1）如图1，当tan∠PAB=1，c=2
时，a= ，b= ；如图2，当∠PAB=30°，c=4时，a= ，b= ；
（归纳证明）
（2）请你观察（1）中的计算结果，猜想a2、b2、c2三者之间的关系，用等式表示出来，并利用图3证明你的结论．
（拓展证明）
（3）如图4，ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=6
，AB=6，求AF的长．
-
科目： 来源： 题型：
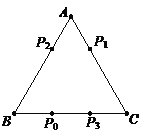
查看答案和解析>>【题目】电子跳蚤游戏盘是如图所示的△ABC，AB=AC=BC=5．如果跳蚤开始时在BC边的P0处，BP0=2．跳蚤第一步从P0跳到AC边的P1（第1次落点）处，且CP1= CP0；第二步从P1跳到AB边的P2（第2次落点）处，且AP2= AP1；第三步从P2跳到BC边的P3（第3次落点）处，且BP3= BP2；…；跳蚤按照上述规则一直跳下去，第n次落点为Pn（n为正整数），则点P2016与点P2017之间的距离为_________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点 A，B的坐标分别为（0，3），（1，0），△ABC是等腰直角三角形，∠ABC＝90°．
（1）图1中，点C的坐标为 ；
(2)如图2，点D的坐标为（0，1），点E在射线CD上，过点B 作BF⊥BE交y轴于点F．
①当点E为线段CD的中点时，求点F的坐标；
②当点E在第二象限时，请直接写出F点纵坐标y的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC的三边AB、BC、CA长分别为30、40、50．其三条角平分线交于点O，则S△ABO ：S△BCO ：S△CAO =______ 。
-
科目： 来源： 题型：
查看答案和解析>>【题目】随着“互联网+”时代的到来，一种新型打车方式受到大众欢迎，该打车方式的总费用由里程费和耗时费组成，其中里程费按x元/公里计算，耗时费按y元/分钟计算（总费用不足9元按9元计价）．小明、小刚两人用该打车方式出行，按上述计价规则，其打车总费用、行驶里程数与打车时间如表：
时间（分钟）
里程数（公里）
车费（元）
小明
8
8
12
小刚
12
10
16
（1）求x，y的值；
（2）如果小华也用该打车方式，打车行驶了11公里，用了14分钟，那么小华的打车总费用为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的袋子中装有红、白两种颜色的小球，这些球除颜色外完全相同，其中红球有
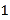个，若从中随机摸出一个球，这个球是白球的概率为
．（
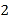）请直接写出袋子中白球的个数．（
）随机摸出一个球后，放回并搅匀，再随机摸出一个球，求两次都摸到相同颜色的小球的概率．（请结合树状图或列表解答）
相关试题
