【题目】如图,直线AB分别与两坐标轴交于点A(6,0),B(0,12),点C的坐标为(3,0)
(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为16,求点P的坐标.
②连结CP,是否存在点P,使△ACP与△AOB相似?若存在,求出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)y=﹣2x+12;(2)①点P(2,8)或(4,4);②存在,点P的坐标为(3,6)或点P(![]() ,
,![]() )
)
【解析】
试题(1)由于A(6,0),B(0,12),利用待定系数法即可求出直线AB的解析式;
(2)①可以设动点P(x,﹣2x+12),由此得到PE=x,PF=﹣2x+12,再利用矩形OEPF的面积为16即可求出点P的坐标;
②存在,分两种情况:第一种由CP∥OB得△ACP∽△AOB,由此即可求出P的坐标;第二种CP⊥AB,根据已知条件可以证明APC∽△AOB,然后利用相似三角形的对应边成比例即可求出PA,再过点P作PH⊥x轴,垂足为H,由此得到PH∥OB,进一步得到△APH∽△ABO,然后利用相似三角形的对应边成比例就可以求出点P的坐标.
解:(1)设直线AB的解析式为y=kx+b,如图1:
依题意,![]() ,
,
∴![]() ,
,
∴y=﹣2x+12;
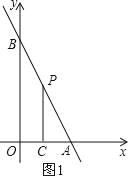
(2)①设动点P (x,﹣2x+12),则PE=x,PF=﹣2x+12,
∴SOEPF=PEPF=x(﹣2x+12)=16,
∴x1=2,x2=4;
经检验x1=2,x2=4都符合题意,
∴点P(2,8)或(4,4);
②存在,分两种情况
∵A(6,0),B(0,12),
∴OA=6,OB=12,AB=6![]()
第一种:CP∥OB,
∴△ACP∽△AOB,
而点C的坐标为(3,0),
∴点P(3,6);
第二种CP⊥AB,
∵∠APC=∠AOB=90°,∠PAC=∠BAO,
∴△APC∽△AOB,
∴![]() ,
,
∴![]() ,
,
∴AP=![]() ,
,
如图2,过点P作PH⊥x轴,垂足为H,
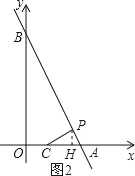
∴PH∥OB,
∴△APH∽△ABO,
∴![]() ,
,
∴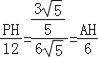 ,
,
∴PH=![]() ,AH=
,AH=![]() ,
,
∴OH=OA﹣AH=6﹣![]() =
=![]() ,
,
∴点P(![]() ,
,![]() ).
).
∴点P的坐标为(3,6)或点P(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量出楼房AC的高度,从距离楼底C处
 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈ ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:数学课上,吴老师在求代数式x2﹣4x+5的最小值时,利用公式a2±2ab+b2=(a±b)2,对式子作如下变形:x2﹣4x+5=x2﹣4x+4+1=(x﹣2)2+1,
因为(x﹣2)2≥0,
所以(x﹣2)2+1≥1,
当x=2时,(x﹣2)2+1=1,
因此(x﹣2)2+1有最小值1,即x2﹣4x+5的最小值为1.
通过阅读,解下列问题:
(1)代数式x2+6x+12的最小值为 ;
(2)求代数式﹣x2+2x+9的最大或最小值;
(3)试比较代数式3x2﹣2x与2x2+3x﹣7的大小,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A坐标(0,6),AC⊥y轴,且AC=AO,点B,C横坐标相同,点D在AC上,tan∠AOD=
 ,若反比例函数y=
,若反比例函数y= (x>0)的图象经过点B、D.
(x>0)的图象经过点B、D.(1)求:k及点B坐标;
(2)将△AOD沿着OD折叠,设顶点A的对称点A1的坐标是A1(m,n),求:代数式m+3n的值以及点A1的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
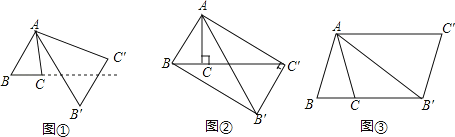
(1)如图①,对△ABC作变换[60°,
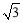 ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形称为“中垂三角形”.设BC=a,AC=b,AB=c.
(特例探究)
(1)如图1,当tan∠PAB=1,c=2
 时,a= ,b= ;
时,a= ,b= ;如图2,当∠PAB=30°,c=4时,a= ,b= ;
(归纳证明)
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(拓展证明)
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=6
 ,AB=6,求AF的长.
,AB=6,求AF的长.
-
科目: 来源: 题型:
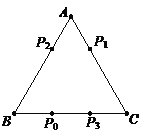
查看答案和解析>>【题目】电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=5.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1= CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2= AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3= BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2016与点P2017之间的距离为_________.
相关试题

