【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等问题.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等问题.
例如:分解因式![]() ;求代数式
;求代数式![]() 的最小值,
的最小值,![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _______.
_______.
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最大值?并求出这个最大值.
有最大值?并求出这个最大值.
(3)利用配方法,尝试解方程![]() ,并求出
,并求出![]() ,
,![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)当
;(2)当![]() 时,原式有最大值,最大值为
时,原式有最大值,最大值为![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)先把![]() 配方,再利用平方差公式分解因式即可;
配方,再利用平方差公式分解因式即可;
(2)把原式配方,根据平方的非负数性质即可得答案;
(3)把原式分组配方,根据平方的非负数性质即可求出a、b的值.
(1)![]()
=x2-4x+4-9
=(x-2)2-32
=(x-2+3)(x-2-3)
=(x+1)(x-5).
故答案为:(x+1)(x-5)
(2)原式![]() ,
,
∵(x+1)2≥0,
∴当![]() 时,原式有最大值,最大值为
时,原式有最大值,最大值为![]() .
.
(3)![]() ,
,
![]() ,
,
 ,
,
∴![]() ,且
,且![]() ,
,
解得:![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列的网格图中.每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元)
5
10
20
50
100
人数(单位:个)
2
4
5
3
1
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
-
科目: 来源: 题型:
查看答案和解析>>【题目】“两果问价”问题出自我国古代算书《四元玉鉴》,原题如下:九百九十九文钱,甜果苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果几个?又问各该几个钱?将题目译成白话文,内容如下:九百九十九文钱买了甜果和苦果共一千个,已知十一文钱可买九个甜果,四文钱可买七个苦果,那么甜果、苦果各买了多少个?买甜果和苦果各需要多少文钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数
 与
与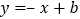 图像的交点在第一象限,则一次函数
图像的交点在第一象限,则一次函数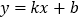 的图像不经过( )
的图像不经过( )A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“
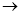 ”方向排列,如
”方向排列,如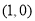 ,
,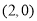 ,
,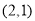 ,
,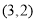 ,
,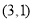 ,
,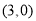 ,
,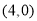 .根据这个规律探索可得,第110个点的坐标为__________.
.根据这个规律探索可得,第110个点的坐标为__________.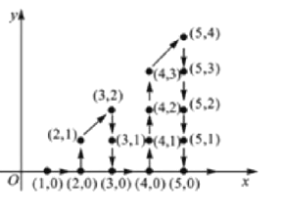
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,
 时注满水槽,水槽内水面的高度
时注满水槽,水槽内水面的高度 与注水时间
与注水时间 之间的函数图像如图2所示.如果将正方体铁块取出,又经过____秒恰好将水槽注满.
之间的函数图像如图2所示.如果将正方体铁块取出,又经过____秒恰好将水槽注满.
相关试题

