【题目】杂技团进行杂技表演,演员从跷跷板右端A处(OA=1米)弹跳到人梯顶端椅子B处,借助其弹性可以将演员弹跳到离地面最高处点P( ![]() ,
, ![]() )
)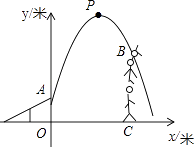
(1)若将其身体(看成一个点)的路线为抛物线的一部分,求抛物线的解析式.
(2)在一次表演中,已知人梯高BC=3.4米,演员弹跳到最高处点P后落到人梯顶端椅子B处算表演成功,为了这次表演成功,人梯离起跳点A的水平距离OC是多少米?请说明理由.
参考答案:
【答案】
(1)
解:设抛物线解析式为y=a(x﹣h)2+k,
∵最高处点P( ![]() ,
, ![]() ),
),
∴h= ![]() ,k=
,k= ![]() ,
,
∴y=a(x﹣ ![]() )2+
)2+ ![]() ,
,
∵OA=1米,
∴点A的坐标为(0,1),
∴1=a× ![]() +
+ ![]() ,
,
解得:a=﹣ ![]() ,
,
∴y=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() =﹣
=﹣ ![]() x2+3x+1;
x2+3x+1;
(2)
解:∵BC=3.4米,
∴B的纵坐标为3.4,
∴3.4=﹣ ![]() x2+3x+1,
x2+3x+1,
解得:x=4或1,
∴人梯离起跳点A的水平距离OC是4米.
【解析】(1)设抛物线解析式为y=a(x﹣h)2+k,由已知条件可知h和k的值,再把点A的坐标代入求出a的值即可;(2)由BC=3.4米,可知点B的纵坐标为3.4,把其纵坐标代入抛物线的解析式求出其横坐标,即可得到人梯离起跳点A的水平距离OC.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
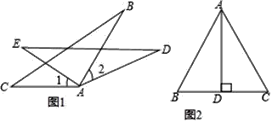
查看答案和解析>>【题目】(1)如图1,AC=AE,∠1=∠2,∠C=∠E.求证:BC=DE.
(2)如图2,在△ABC中,AB=AC,D为BC中点,∠BAD=30°,求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是抛物线y=x2﹣4x+3上的一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与直线y=0相切时,点P的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知等边△OAB的顶点A在反比例函数y=
 (x>0)图象上,当等边△OAB的顶点B在坐标轴上时,求等边△OAB顶点A的坐标和△OAB的面积.
(x>0)图象上,当等边△OAB的顶点B在坐标轴上时,求等边△OAB顶点A的坐标和△OAB的面积. 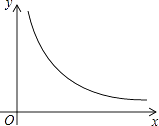
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在平面直角坐标系中,每个小正方形的边长为1,△ABC的顶点都在格点上,点A的坐标为(-3,2).请按要求分别完成下列各小题:
(1)把△ABC向下平移7个单位,再向右平移7个单位,得到△A1B1C1,画出△A1B1C1;
(2)画出△A1B1C1关于x轴对称的△A2B2C2;
画出△A1B1C1关于y轴对称的△A3B3C3;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在羊年春节晚会上举行一个游戏,规则如下:有4张背面相同的卡片,正面分别是喜羊羊、美羊羊、慢羊羊、懒羊羊的头像,分别对应1000元、600元、400元、200元的奖金,现将4张纸牌洗匀后背面朝上摆放到桌上,让员工抽取,每人有两次抽奖机会,两次抽取的奖金之和作为公司发的年终奖金.现有两种抽取的方案:①小芳抽取方案是:直接从四张牌中抽取两张.②小明抽取的方案是:先从四张牌中抽取一张后放回去,再从四张中再抽取一张.你认为是小明抽到的奖金不少于1000元的概率大还是小芳抽取到的奖金不少于1000元的概率大?请用树形图或列表法进行分析说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.

(1)求证:CD为⊙O的切线;
(2)若CD=2AD,⊙O的直径为20,求线段AC、AB的长.
相关试题

