搜索
【题目】如图，P是抛物线y=x2﹣4x+3上的一点，以点P为圆心、1个单位长度为半径作⊙P，当⊙P与直线y=0相切时，点P的坐标为 ． 
参考答案：
【答案】（2+ 
，1）或（2﹣ ，1）或（2，﹣1）
【解析】解：当y=1时，x2﹣4x+3=1，
解得：x=2± ，
∴P（2+ ，1）或（2﹣ ，1），
当y=﹣1时，x2﹣4x+3=﹣1，
解得：x1=x2=2，
∴P（2，﹣1），
则点P的坐标为：（2+ ，1）或（2﹣ ，1）或（2，﹣1）．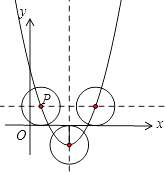
⊙P与直线y=0相切时就是：⊙P与x轴相切，半径为1个单位长度，即点P的纵坐标|y|=1，根据P是抛物线y=x2﹣4x+3上的一点，代入计算出x的值，并写出点P的坐标，一共有3种可能．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将油箱注满k升油后，轿车行驶的总路程S（单位：千米）与平均耗油量a（单位：升/千米）之间是反比例函数关系S=
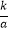（k是常数，k≠0）．已知某轿车油箱注满油后，以平均耗油量为每千米耗油0.1升的速度行驶，可行驶760千米，当平均耗油量为0.08升/千米时，该轿车可以行驶千米． -
科目： 来源： 题型：
查看答案和解析>>【题目】太原市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位．公共自行车车桩的截面示意图如图所示，AB⊥AD，AD⊥DC，点B，C在EF上，EF∥HG，EH⊥HG，AB=75cm，AD=24cm，BC=25cm，EH=4cm，则点A到地面的距离是 cm．
-
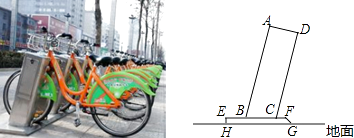
科目： 来源： 题型：
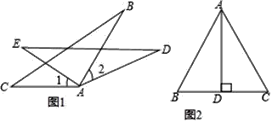
查看答案和解析>>【题目】（1）如图1，AC=AE，∠1=∠2，∠C=∠E．求证：BC=DE．
（2）如图2，在△ABC中，AB=AC，D为BC中点，∠BAD=30°，求∠C的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知等边△OAB的顶点A在反比例函数y=
（x＞0）图象上，当等边△OAB的顶点B在坐标轴上时，求等边△OAB顶点A的坐标和△OAB的面积．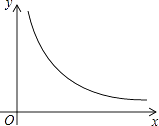 
-
科目： 来源： 题型：
查看答案和解析>>【题目】杂技团进行杂技表演，演员从跷跷板右端A处（OA=1米）弹跳到人梯顶端椅子B处，借助其弹性可以将演员弹跳到离地面最高处点P（
， 
）
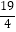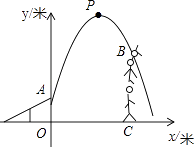
（1）若将其身体（看成一个点）的路线为抛物线的一部分，求抛物线的解析式．
（2）在一次表演中，已知人梯高BC=3.4米，演员弹跳到最高处点P后落到人梯顶端椅子B处算表演成功，为了这次表演成功，人梯离起跳点A的水平距离OC是多少米？请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知：在平面直角坐标系中，每个小正方形的边长为1，△ABC的顶点都在格点上，点A的坐标为（－3，2）.请按要求分别完成下列各小题：
（1）把△ABC向下平移7个单位，再向右平移7个单位，得到△A1B1C1，画出△A1B1C1；
（2）画出△A1B1C1关于x轴对称的△A2B2C2；
画出△A1B1C1关于y轴对称的△A3B3C3；
（3）求△ABC的面积.
相关试题
