【题目】二次函数y=ax ![]() +bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①抛物线与x轴的另一个交点是(5,0);②4a+c>2b;③4a+b=0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )
+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①抛物线与x轴的另一个交点是(5,0);②4a+c>2b;③4a+b=0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )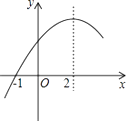
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】B
【解析】①∵二次函数y=ax2+bx+c(a≠0)与x轴的一个交点为(-1,0)且对称轴为直线x=2,
∴另一个交点坐标为(5,0),故①正确;②∵二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2, ∴当x=-2时,y=4a-2b+c<0, ∴4a+c<2b,故②错误;③∵对称轴为=- ![]() , ∴
, ∴ ![]() =2, ∴4a+b=0,故③正确;④当x<2时, y的值随x值的增大而增大, 当x>2时, y的值随x值的增大而减小,故④错误.
=2, ∴4a+b=0,故③正确;④当x<2时, y的值随x值的增大而增大, 当x>2时, y的值随x值的增大而减小,故④错误.
故答案为:B.
根据抛物线的对称性,知道次函数y=ax2+bx+c(a≠0)与x轴的一个交点为(-1,0)且对称轴为直线x=2,从而得出其与x轴的另一个交点坐标为(5,0) ;抛物线当x=-2时,其对应的函数图像在x轴的下方,即y=4a-2b+c<0, 故4a+c<2b ;根据抛物线的对称轴公式得出方程就可得出4a+b=0 ;利用抛物线的开口方向,及顶点横坐标知 ;当x<2时, y的值随x值的增大而增大, 当x>2时, y的值随x值的增大而减小 ;从而就可以对几个答案一一判断。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形
 中,
中, .
.
(1)如图1,点
 为线段
为线段 的中点,连接
的中点,连接 ,
, .若
.若 ,求线段
,求线段 的长.
的长.(2)如图2,
 为线段
为线段 上一点(不与
上一点(不与 ,
, 重合),以
重合),以 为边向上构造等边三角形
为边向上构造等边三角形 ,线段
,线段 与
与 交于点
交于点 ,连接
,连接 ,
, ,
, 为线段
为线段 的中点.连接
的中点.连接 ,
, 判断
判断 与
与 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.(3)在(2)的条件下,若
 ,请你直接写出
,请你直接写出 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,
 ,
, 是
是 轴正半轴上一点,
轴正半轴上一点, ,若
,若 与
与 互为相反数.
互为相反数.

(1)求
 的值;
的值;(2)如图2,
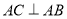 交
交 轴于
轴于 ,以
,以 为边的正方形
为边的正方形 的对角线
的对角线 交
交 轴于
轴于 .
.①求证:
 ;
;②记
 ,
, ,求
,求 的值.
的值. -
科目: 来源: 题型:
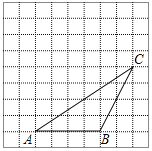
查看答案和解析>>【题目】如图,在每个小正方形边长为1的方格纸中,△ADC的顶点都在方格纸格点上,将△ABC向左平移1格.再向上平移1格,
(1)在图中画出平移后的△A′B′C′;
(2)画出AB边上的高CE;
(3)过点A画BC的平行线;
(4)在图中,若△BCQ的面积等于△BCA的面积.则图中满足条件且异于点A的个点Q共有_____个.(注:格点指网格线的交点)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠D=∠B=90°,AE平分∠DAB,CF平分∠DCB
(1)若∠DAB=72°,∠2= °,∠3= °;
(2)求证:AE∥CF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某新建小区要在一块等边三角形内修建一个圆形花坛.

(1)要使花坛面积最大,请你用尺规画出圆形花坛示意图;(保留作图痕迹,不写做法)
(2)若这个等边三角形的周长为36米,请计算出花坛的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;
①若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)
②若AB为任意值,且①中的S的值为定值,求a与b的关系.

相关试题

