【题目】一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;
①若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)
②若AB为任意值,且①中的S的值为定值,求a与b的关系.

参考答案:
【答案】(1)(2a+b)(2b+a)=2a2+5ab+2b2;(2)(a﹣b)2,(a﹣b)2=(a+b)2﹣4ab;(3)①S=4ab﹣4b+12a﹣b2;②3a=b.
【解析】
(1)根据图形面积可知(2a+b)(2b+a)=2a2+5ab+2b2;
(2)根据阴影部分面积可以是大正方形面积减去四个长方形面积,
得到(a-b)2=(a+b)2-4ab;
(3)①大长方形的面积=(3a+b)(4+b)=7ab+4×3a+4×3a-S;
②设AB=m,大长方形的面积=(3a+b)(m+b)=7ab+3ma+3ma-S,3a-b=0;
解:(1)根据图可知长方形面积有(2a+b)(2b+a)=2a2+5ab+2b2;
故答案为(2a+b)(2b+a)=2a2+5ab+2b2;
(2)④图中阴影部分面积是(a﹣b)2,
根据阴影部分面积可以是大正方形面积减去四个长方形面积,
∴(a﹣b)2=(a+b)2﹣4ab,
故答案为(a﹣b)2,(a﹣b)2=(a+b)2﹣4ab;
(3)①∵AB=4,长方形AGMB的面积与长方形EDHN的面积的差为S,
∴大长方形的面积=(3a+b)(4+b)=7ab+4×3a+4×3a﹣S,
∴S=4ab﹣4b+12a﹣b2;
②设AB=m,
∴大长方形的面积=(3a+b)(m+b)=7ab+3ma+3ma﹣S,
∴S=4ab﹣b2+m(3a﹣b),
∵若AB为任意值,且①中的S的值为定值,
∴3a=b.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax
 +bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①抛物线与x轴的另一个交点是(5,0);②4a+c>2b;③4a+b=0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )
+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①抛物线与x轴的另一个交点是(5,0);②4a+c>2b;③4a+b=0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )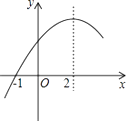
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠D=∠B=90°,AE平分∠DAB,CF平分∠DCB
(1)若∠DAB=72°,∠2= °,∠3= °;
(2)求证:AE∥CF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某新建小区要在一块等边三角形内修建一个圆形花坛.

(1)要使花坛面积最大,请你用尺规画出圆形花坛示意图;(保留作图痕迹,不写做法)
(2)若这个等边三角形的周长为36米,请计算出花坛的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AB=AC,∠B=50°,P 是边 AB 上的一个动点(不与顶点 A 重合),则∠BPC 的度数可能是

A. 50° B. 80° C. 100° D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个口袋中有4个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸取一个小球然后放回,再随机地摸出一个小球,求下列事件的概率:
(1)两次取的小球的标号相同
(2)两次取的小球的标号的和等于4 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1所示,△ABC中,∠ACB的角平分线CF与∠EAC的角平分线AD的反向延长线交于点F;
①若∠B=90°则∠F= ;
②若∠B=a,求∠F的度数(用a表示);
(2)如图2所示,若点G是CB延长线上任意一动点,连接AG,∠AGB与∠GAB的角平分线交于点H,随着点G的运动,∠F+∠H的值是否变化?若变化,请说明理由;若不变,请求出其值.

相关试题

