【题目】如图1,在平面直角坐标系中,![]() ,
,![]() 是
是![]() 轴正半轴上一点,
轴正半轴上一点,![]() ,若
,若![]() 与
与![]() 互为相反数.
互为相反数.


(1)求![]() 的值;
的值;
(2)如图2,![]() 交
交![]() 轴于
轴于![]() ,以
,以![]() 为边的正方形
为边的正方形![]() 的对角线
的对角线![]() 交
交![]() 轴于
轴于![]() .
.
①求证:![]() ;
;
②记![]() ,
,![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)①见解析,②3
;(2)①见解析,②3
【解析】
(1)根据相反数的概念得出方程![]() ,求出
,求出![]() 的值,作AG⊥OB于G,利用含30度角的直角三角形的性质即可求得答案;
的值,作AG⊥OB于G,利用含30度角的直角三角形的性质即可求得答案;
(2)①延长AC交y轴于点Q,作AP⊥OA交OB于P,利用“ASA”证得△OAQ![]() △PAB,得到AQ= AB,
△PAB,得到AQ= AB,![]() ,QC=2OC,再利用线段的和差即可证明;
,QC=2OC,再利用线段的和差即可证明;
②连接QF,利用“SAS”证得△FAQ![]() △FAB,得到
△FAB,得到![]() ,从而证得结论.
,从而证得结论.
(1)∵![]() 和
和![]() 互为相反数,
互为相反数,
∴![]() ,
,
∴![]() ,
,![]()
![]() ,
,
∴![]() ,
,
如图:作AG⊥OB于G,
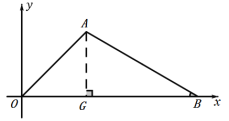
∵点A的坐标为(![]() ,
,![]() ),即A (
),即A (![]() ,
,![]() ),
),
∴AG=OG=2,
在Rt![]() BAG中,∠ABG=30
BAG中,∠ABG=30![]() ,AG=2,
,AG=2,
∴AB=2AG=4,
BG=![]() ,
,
∴BO= OG+ BG=2+![]() ,
,
∴![]() ;
;
(2)①延长AC交![]() 轴于点Q,作AP⊥OA交OB于P,如图:
轴于点Q,作AP⊥OA交OB于P,如图:
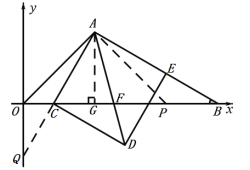
由(1)得AG=OG=2,AG⊥OB,
∴∠AOG=45![]() ,
,
∵AP⊥OA,
∴∠APO=90![]() -∠AOG =45
-∠AOG =45![]() ,
,
∴∠APO=∠AOG=45![]() ,
,
∴AO=AP,∠APB=180![]() -45
-45![]() =135
=135![]() ,
,
∠AOQ=90![]() +45
+45![]() =135
=135![]() ,
,
∴∠APB=∠AOQ,
∵AP⊥OA,AC⊥AB,
∴∠OAP=∠CAB=90![]() ,
,
∴∠OAQ+∠CAP =∠PAB+∠CAP =90![]() ,
,
∴∠OAQ=∠PAB,
在△OAQ和△PAB中,
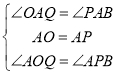 ,
,
∴△OAQ![]() △PAB(ASA),
△PAB(ASA),
∴AQ= AB,![]() ,
,
在Rt![]() OQC中,∠OQC=30
OQC中,∠OQC=30![]() ,
,
∴QC=2OC,
∵四边形ACDE为正方形,
∴AC=AE,
∴BE=AB-AE=AQ-AC=QC=2OC;
②如图,连接QF,
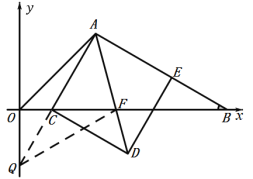
∵四边形ACDE为正方形,AD为对角线,
∴![]() ,
,
由①得:AQ= AB,![]() ,QC=2OC,
,QC=2OC,
∴![]() ,
,
在△FAQ和△FAB中,
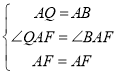 ,
,
∴△FAQ![]() △FAB (SAS),
△FAB (SAS),
∴QF=BF,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“每天在校体育活动时间”的问题随机抽样调查了321名初中学生.根据调查结果将学生每天在校体育活动时间t(小时)分成
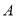 ,
,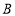 ,
,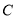 ,
,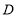 四组,并绘制了统计图(部分).
四组,并绘制了统计图(部分).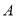 组:
组: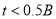 组:
组: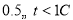 组:
组: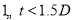 组:
组: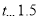

请根据上述信息解答下列问题:
(1)
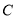 组的人数是 ;
组的人数是 ;(2)本次调查数据的中位数落在 组内;
(3)若该市约有12840名初中学生,请你估算其中达到国家规定体育活动时间的人数大约有多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, 是
是 的中点,将
的中点,将 沿
沿 折叠后得到
折叠后得到 ,点
,点 在矩形
在矩形 内部,延长
内部,延长 交
交 于点G.
于点G.
(1)猜想线段
 与
与 有何数量关系?并证明你的结论;
有何数量关系?并证明你的结论;(2)若
 ,
, ,求线段
,求线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形
 中,
中, .
.
(1)如图1,点
 为线段
为线段 的中点,连接
的中点,连接 ,
, .若
.若 ,求线段
,求线段 的长.
的长.(2)如图2,
 为线段
为线段 上一点(不与
上一点(不与 ,
, 重合),以
重合),以 为边向上构造等边三角形
为边向上构造等边三角形 ,线段
,线段 与
与 交于点
交于点 ,连接
,连接 ,
, ,
, 为线段
为线段 的中点.连接
的中点.连接 ,
, 判断
判断 与
与 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.(3)在(2)的条件下,若
 ,请你直接写出
,请你直接写出 的最小值.
的最小值. -
科目: 来源: 题型:
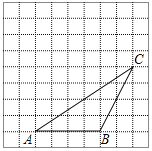
查看答案和解析>>【题目】如图,在每个小正方形边长为1的方格纸中,△ADC的顶点都在方格纸格点上,将△ABC向左平移1格.再向上平移1格,
(1)在图中画出平移后的△A′B′C′;
(2)画出AB边上的高CE;
(3)过点A画BC的平行线;
(4)在图中,若△BCQ的面积等于△BCA的面积.则图中满足条件且异于点A的个点Q共有_____个.(注:格点指网格线的交点)
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax
 +bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①抛物线与x轴的另一个交点是(5,0);②4a+c>2b;③4a+b=0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )
+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①抛物线与x轴的另一个交点是(5,0);②4a+c>2b;③4a+b=0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )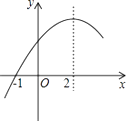
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠D=∠B=90°,AE平分∠DAB,CF平分∠DCB
(1)若∠DAB=72°,∠2= °,∠3= °;
(2)求证:AE∥CF.

相关试题

