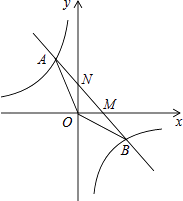
【题目】如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数y2=﹣ ![]() 的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
(1)求一次函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出y1>y2时x的取值范围.
参考答案:
【答案】
(1)解:设点A坐标为(﹣2,m),点B坐标为(n,﹣2)
∵一次函数y1=kx+b(k≠0)的图象与反比例函数y2=﹣ ![]() 的图象交于A、B两点
的图象交于A、B两点
∴将A(﹣2,m)B(n,﹣2)代入反比例函数y2=﹣ ![]() 可得,m=4,n=4
可得,m=4,n=4
∴将A(﹣2,4)、B(4,﹣2)代入一次函数y1=kx+b,可得
![]() ,解得
,解得 ![]()
∴一次函数的解析式为y1=﹣x+2;
(2)解:在一次函数y1=﹣x+2中,
当x=0时,y=2,即N(0,2);当y=0时,x=2,即M(2,0)
∴S△AOB=S△AON+S△MON+S△MOB= ![]() ×2×2+
×2×2+ ![]() ×2×2+
×2×2+ ![]() ×2×2=2+2+2=6;
×2×2=2+2+2=6;
(3)解:根据图象可得,当y1>y2时,x的取值范围为:x<﹣2或0<x<4
【解析】(1)根据已知点A的横坐标和点B的纵坐标都是﹣2.代入反比例函数解析式求出点A、B的坐标,再利用待定系数法求出一次函数的解析式即可。
(2)先求出直线AB与x轴、y轴的交点坐标,再根据S△AOB=S△AON+S△MON+S△MOB,即可求解,或根据S△AOB=S△AON+S△BON或根据S△AOB=S△AOM+S△BOM求解即可。
(3)观察直线x=-2、直线x=4、y轴将两函数的图像分成四部分,一次函数的图像要高于反比例函数的图像,即可求出此时自变量的取值范围。
【考点精析】本题主要考查了确定一次函数的表达式和反比例函数的图象的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为节约能源,某单位按以下规定收取每月电费:用电不超过140度,按每度
 元收费,如果超过140度,超过部分按每度
元收费,如果超过140度,超过部分按每度 元收费.
元收费. 若某住户六月份的用电量是130度,该用户六月份应缴多少电费?
若某住户六月份的用电量是130度,该用户六月份应缴多少电费? 若该住户七月份的用电量是200度,该用户七月份应缴多少电费?
若该住户七月份的用电量是200度,该用户七月份应缴多少电费? 若某住户十月份的用电量是a度,该用户十月份应缴多少电费?
若某住户十月份的用电量是a度,该用户十月份应缴多少电费? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC与△CDE都是等边三角形,点B、C、D在同一直线上,AD与BE相交于点G,BE与AC相交于点F,AD与CE相交于点H,则下列结论:①△ACD≌△BCE;②∠AGB=60°;③BF=AH;④△CFH是等边三角形;⑤连CG,则∠BGC=∠DGC ;⑥EG+GC=GD. 其中正确的有________.(只要写序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定“中小学生每天在校体育活动时间不低于1小时(h)”,某市就“你每天在校体育活动时间是多少?”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:A组:t<0.5h;B组:0.5h≤t<1h;C组:1h≤t<1.5h;D组:t≥1.5h.
请根据上述信息解答下列问题
(1)补全条形统计图;
(2)某市约有25000名初中学生,请你结合以上数据进行
①估计达到国家规定体育活动时间的人数是多少?
②如果要估算本市初中生每天在校体育活动时间是多少,你认为选择众数、中位数和平均数三个量中的哪个更合适?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移得到△A1B1C1,且点P的对应点为P1(a+5,b+4).
(1)写出△ABC的三个顶点的坐标;
(2)请在平面直角坐标系中画出△A1B1C1.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售的一款空调机每台的标价是1635元,在一次促销活动中,按标价的八折销售,仍可盈利9%.
(1)求这款空调每台的进价(利润率= =
=  ).
).
(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.求证:BF=2AE.

相关试题

