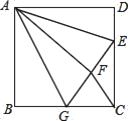
【题目】如图,已知△ABC与△CDE都是等边三角形,点B、C、D在同一直线上,AD与BE相交于点G,BE与AC相交于点F,AD与CE相交于点H,则下列结论:①△ACD≌△BCE;②∠AGB=60°;③BF=AH;④△CFH是等边三角形;⑤连CG,则∠BGC=∠DGC ;⑥EG+GC=GD. 其中正确的有________.(只要写序号)

参考答案:
【答案】①②③④⑤⑥
【解析】
利用等边三角形的性质得出条件,可证明:△BCE≌△ACD;利用△BCE≌△ACD得出∠CBF=∠CAH,再运用平角定义得出∠BCF=∠ACH,进而得出△BCF≌△ACH因此BF=AH.由CF=CH和∠ACH=60°根据“有一个角是60°的三角形是等边三角形可得△CFH是等边三角形.连接CG,过C作CI⊥BE于I,CJ⊥AD于J.由全等三角形对应边上的高相等得到CI=CJ,由角平分线的判定定理得到GC平分∠BGD.
在GD上截取GM=GE,连接EM.由∠EGM=∠AGB=60°,得到△EGM是等边三角形,得到ME=GE,∠GEM=60°.通过证明△GEC≌△MED,得到GC=MD,即可得到GD=GM+MD=GE+CG.
∵∠BCA=∠DCE=60°,∴∠ACE=60°,∴∠BCE=∠ACD.在△BCE和△ACD中,∵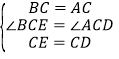 ,∴△BCE≌△ACD(SAS);故①正确;
,∴△BCE≌△ACD(SAS);故①正确;
∵△BCE≌△ACD,∴∠CBF=∠CAH.
∵∠BFC=∠AFG,∴∠AGB=∠ACB=60°,故②正确;
在△BCF和△ACH中,∵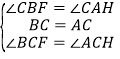 ,∴△BCF≌△ACH(ASA),∴CF=CH,BF=AH;故③正确;
,∴△BCF≌△ACH(ASA),∴CF=CH,BF=AH;故③正确;
∵CF=CH,∠ACH=60°,∴△CFH是等边三角形;故④正确;
连接CG.过C作CI⊥BE于I,CJ⊥AD于J.
∵△BCE≌△ACD,∴CI=CJ,∴GC平分∠BGD,∴∠BGC=∠DGC.故⑤正确.
在GD上截取GM=GE,连接EM.
∵∠EGM=∠AGB=60°,∴△EGM是等边三角形,∴ME=GE,∠GEM=60°.
∵∠CED=60°,∴∠GEC=∠MED.在△GEC和△MED中,∵GE=ME ,∠GEC=∠MED,CE=DE,∴△GEC≌△MED,∴GC=MD,∴GD=GM+MD=GE+CG.故⑥正确.
故答案为:①②③④⑤⑥.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 和点
和点 在数轴上对应的数分别为
在数轴上对应的数分别为 和
和 ,且
,且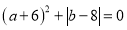 .
.
(1)求线段
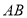 的长;
的长;(2)点
 在数轴上所对应的数为
在数轴上所对应的数为 ,且
,且 是方程
是方程 的解,点
的解,点 在线段
在线段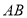 上,并且
上,并且
 ,请求出点
,请求出点 在数轴上所对应的数;
在数轴上所对应的数;(3)在(2)的条件下,线段
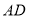 和
和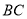 分别以
分别以 个单位长度/秒和
个单位长度/秒和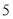 个单位长度/秒的速度同时向右运动,运动时间为
个单位长度/秒的速度同时向右运动,运动时间为 秒,
秒, 为线段
为线段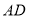 的中点,
的中点, 为线段
为线段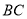 的中点,若
的中点,若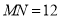 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论: ①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=28.8. 其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】为节约能源,某单位按以下规定收取每月电费:用电不超过140度,按每度
 元收费,如果超过140度,超过部分按每度
元收费,如果超过140度,超过部分按每度 元收费.
元收费. 若某住户六月份的用电量是130度,该用户六月份应缴多少电费?
若某住户六月份的用电量是130度,该用户六月份应缴多少电费? 若该住户七月份的用电量是200度,该用户七月份应缴多少电费?
若该住户七月份的用电量是200度,该用户七月份应缴多少电费? 若某住户十月份的用电量是a度,该用户十月份应缴多少电费?
若某住户十月份的用电量是a度,该用户十月份应缴多少电费? -
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定“中小学生每天在校体育活动时间不低于1小时(h)”,某市就“你每天在校体育活动时间是多少?”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:A组:t<0.5h;B组:0.5h≤t<1h;C组:1h≤t<1.5h;D组:t≥1.5h.
请根据上述信息解答下列问题
(1)补全条形统计图;
(2)某市约有25000名初中学生,请你结合以上数据进行
①估计达到国家规定体育活动时间的人数是多少?
②如果要估算本市初中生每天在校体育活动时间是多少,你认为选择众数、中位数和平均数三个量中的哪个更合适?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数y2=﹣
 的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
(1)求一次函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出y1>y2时x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移得到△A1B1C1,且点P的对应点为P1(a+5,b+4).
(1)写出△ABC的三个顶点的坐标;
(2)请在平面直角坐标系中画出△A1B1C1.

相关试题

