【题目】边长为4、中心为![]() 的正方形
的正方形![]() 如图所示,动点
如图所示,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒1个单位长度的速度运动到点
以每秒1个单位长度的速度运动到点![]() 时停止,动点
时停止,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒2个单位长度的速度运动一周停止,若点
以每秒2个单位长度的速度运动一周停止,若点![]() 同时开始运动,点
同时开始运动,点![]() 的运动时间为
的运动时间为![]()
![]() ,当
,当![]() 时,满足
时,满足![]() 的点
的点![]() 的位置有( )
的位置有( )

A.6个B.7个C.8个D.9个
参考答案:
【答案】B
【解析】
依次取![]() 的中点
的中点![]() ,连接
,连接![]() .由题意可知,当点
.由题意可知,当点![]() 与点
与点![]() 到各自所在边的中点的距离相等时,
到各自所在边的中点的距离相等时,![]() ,则有六种情况,分类列式计算求出t的值,即可解答本题.
,则有六种情况,分类列式计算求出t的值,即可解答本题.
解:依次取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
根据题意,得点![]() 运动的路程为
运动的路程为![]() ,当
,当![]() 时,点
时,点![]() 运动的路程为
运动的路程为![]() .
.
分析题意可知,当点![]() 与点
与点![]() 到各自所在边的中点的距离相等时,
到各自所在边的中点的距离相等时,![]() .
.
当![]() 时,显然
时,显然![]() ;
;
②当![]() 时,如图(1),点
时,如图(1),点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]()
![]() ,
,
由![]() ,得
,得![]() ;
;
③当![]() 时,如图(2),点
时,如图(2),点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() ,
,
由![]() ,得
,得![]() 或
或![]() ;
;
④当![]() 时,如图(3),点
时,如图(3),点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() ,
,
由![]() ,得
,得![]() (舍去)或
(舍去)或![]() ;
;
⑤当![]() 时,如图(4),点
时,如图(4),点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() ,
,
由![]() ,得
,得![]() 或
或![]() ;
;
⑥当![]() 时,点
时,点![]() 停在点
停在点![]() 处,因此当
处,因此当![]() 时,
时,![]() ,只有
,只有![]() 时满足
时满足![]() .
.
综上,满足条件
的点![]() 的位置有7个,
的位置有7个,
故选:B.
-
科目: 来源: 题型:
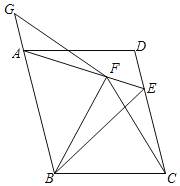
查看答案和解析>>【题目】在平行四边形ABCD中,以AB为边作等边△ABE,点E在CD上,以BC为边作等边△BCF,点F在AE上,点G在BA延长线上且FG=FB.
(1)若CD=6,AF=3,求△ABF的面积;
(2)求证:BE=AG+CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】初中数学代数知识中,方程、函数、不等式存在着紧密的联系,请阅读下列两则材料,回答问题:
利用函数图象找方程
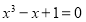 解的范围.设函数
解的范围.设函数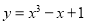 ,当
,当 时,
时,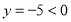 ;当
;当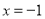 时,
时,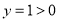 .则函数
.则函数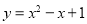 的图象经过两个点
的图象经过两个点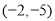 与
与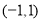 ,而点
,而点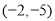 在
在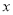 轴下方,点
轴下方,点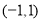 在
在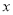 轴上方,则该函数图象与
轴上方,则该函数图象与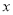 轴交点横坐标必大于-2,小于-1.故,方程
轴交点横坐标必大于-2,小于-1.故,方程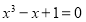 的有解,且该解的范围为
的有解,且该解的范围为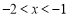 .
.材料二:
解一元二次不等式
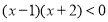 .由“异号两数相乘,结果为负可得:
.由“异号两数相乘,结果为负可得:情况①
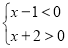 ,得
,得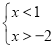 ,则
,则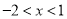
情况②
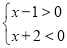 ,得
,得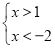 ,则无解
,则无解故,
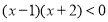 的解集为
的解集为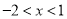 .
.(1)请根据材料一解决问题:已知方程
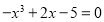 有唯一解
有唯一解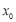 ,且
,且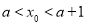 (
(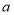 为整数),求整数
为整数),求整数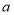 的值.
的值. (2)请结合材料一与材料二解决问题:若关于
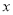 的方程
的方程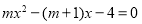 的解分别为
的解分别为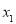 ,
,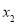 ,且
,且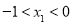 ,
,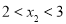 ,求
,求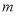 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=x2﹣3与x轴交于AB两点(点A在点B的右侧),与y轴交于点C,连接AC.点Q是线段AC上的动点,过Q作直线l∥x轴,直线1与∠BAC的平分线交于点M,与∠CAx的平分线交于点N.
(1)P是直线AC下方抛物线上一动点,连接PA,PC,当△PAC的面积最大时,求PQ+
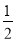 AM的最小值;
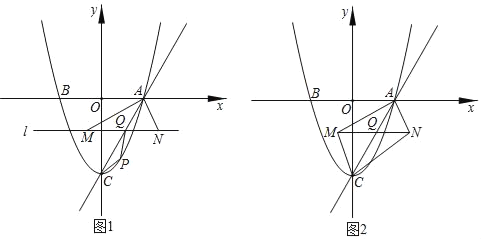
AM的最小值;(2)如图2,连接MC,NC,当四边形AMCN为矩形时,将△AMN沿着直线AC平移得到△A'M'N',边A'M'所在的直线与y轴交于D点,若△DM'N'为等腰三角形时,求OD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
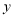 关于
关于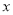 的二次函数
的二次函数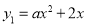 和一次函数
和一次函数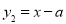 ,若函数
,若函数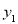 的图象始终在函数
的图象始终在函数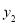 的图象的一侧,则常数
的图象的一侧,则常数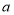 的取值范围是__________.
的取值范围是__________. -
科目: 来源: 题型:
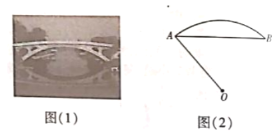
查看答案和解析>>【题目】1400多年前,我国隋代建造的石拱桥——赵州桥(如图(1)),是我国古代人民勤劳与智慧的结晶.如图(2)是它的简化示意图,主桥拱是
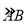 ,拱高(
,拱高(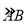 的中点到弦
的中点到弦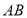 的距离)为
的距离)为 .
. 
(1)在图(2)中(点
 为圆心),用尺规作图作出
为圆心),用尺规作图作出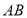 的中点
的中点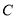 .(不要求写作法,但保留作图痕迹)
.(不要求写作法,但保留作图痕迹)(2)若
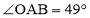 ,求主桥拱的跨度
,求主桥拱的跨度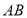 的长.(结果精确到
的长.(结果精确到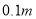 参考数据:
参考数据: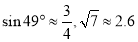 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解禁毒知识宣传的效果,针对全校学生进行了一次测试,并随机抽取 了部分学生的测试成绩(满分100分,最低分为60分,80分及以上为优秀),统计后绘制成如下不完整的

请根据以上信息,解答下列问题:
(1)表中
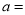 __________,
__________,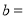 _________;
_________;(2)请补全频数分布直方图;
(3)若该校有学生2100人,试估计分数达到优秀的有多少人;
(4)学校准备从得分最高的5名学生(3男2女)中,随机挑选2名学生去参加市里举办的禁毒知识竞赛.小明说:“因为男生人数是女生人数的
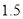 倍,所以选中的2名学生都是男生的概率是选中的2名学生都是女生的概率的
倍,所以选中的2名学生都是男生的概率是选中的2名学生都是女生的概率的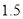 倍.”他的说法正确吗?请判断并说明理由.
倍.”他的说法正确吗?请判断并说明理由.
相关试题

