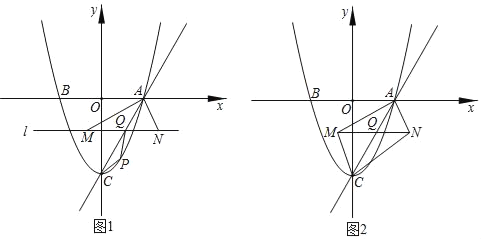
【题目】如图1,抛物线y=x2﹣3与x轴交于AB两点(点A在点B的右侧),与y轴交于点C,连接AC.点Q是线段AC上的动点,过Q作直线l∥x轴,直线1与∠BAC的平分线交于点M,与∠CAx的平分线交于点N.
(1)P是直线AC下方抛物线上一动点,连接PA,PC,当△PAC的面积最大时,求PQ+![]() AM的最小值;
AM的最小值;
(2)如图2,连接MC,NC,当四边形AMCN为矩形时,将△AMN沿着直线AC平移得到△A'M'N',边A'M'所在的直线与y轴交于D点,若△DM'N'为等腰三角形时,求OD的长.
参考答案:
【答案】(1)![]() ;(2) OD的长为2或6或
;(2) OD的长为2或6或![]() .
.
【解析】
(1)用割补法求得△PAC面积的表达式,获得点P的坐标,利用30°构造AM为斜边的直角三角形,转换![]() AM的关系,可证点P到x轴的距离即为PQ+
AM的关系,可证点P到x轴的距离即为PQ+![]() AM的最小值;
AM的最小值;
(2)当四边形AMCN为矩形时,根据矩形的性质点Q为AC与MN的中点,△AMN的三边长度固定,当△DM'N'为等腰三角形时,以D、M'、N'为顶点分三类进行讨论,以线段相等作方程,求得OD的长.
解:(1)由已知可得![]()
设P(m,m2﹣3)
S△PAC=S△POC+S△AOP﹣S△AOC=![]()
当m=![]() 时,△PAC的面积有最大值,此时点P坐标
时,△PAC的面积有最大值,此时点P坐标![]()
如图,作AH⊥MN,
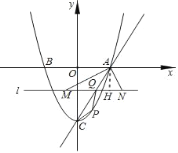
AH=![]() AM
AM
AH长为点Q到x轴的距离
PQ+![]() AM=PQ+AH=
AM=PQ+AH=![]()
(2)当四边形AMCN为矩形时,MN=AC,点Q为AC与MN中点
有题意可知,直线AC的解析式l1为y=![]() x﹣3
x﹣3
过点M与AC平行的直线解析式l2为y=![]() x
x
过点N与AC平行的直线解析式l3为y=![]() x﹣6
x﹣6
直线AM的解析式l4为![]()
设点N'(n,![]() n﹣6),M'(n﹣2
n﹣6),M'(n﹣2![]() ,
,![]() n﹣6)
n﹣6)
设直线A'M'的解析式为![]()
将点M'代入可得![]()
直线A'M'的解析式为![]()
则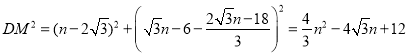
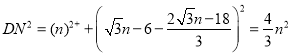
![]()
①当DM'=DN'时,DM'2=DN'2
![]()
解得n=![]()
OD=2
②当DM'=M'N'时,DM'2=M'N'2
![]()
解得n=0或3![]()
OD=6或0
③当DN'=M'N'时,DN'2=M'N'2
![]()
解得n=±3
OD=2![]()
综上所述,OD的长为2或6或2![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年10月18日,党的十九大报告提出“乡村振兴”战略,之后各地发展乡村旅游,某村在2018年3月1日首次举办“百花节”,开园免费赏花,于是大批游客涌入该村赏花,吃农家饭买土特产,平均每人消费100元.
(1)据统计,某个周六早上开园后平均每小时有500人进园,两小时后,平均每小时有100人离园,园区规定,当园区内游客人数达到3000时,将停止进园,那么从开园起经过多少小时后停止进园?
(2)该村对园区加大建设和宣传力度,2019年3月1日,第二届“百花节”如期开园,同时规定进园门票费为每人60元,受各种因素影响,与2018年同期相比,人数在20000的基础上降低了a%,除门票外平均每人消费金额增长了
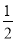 a%,园区总收入增长了
a%,园区总收入增长了 a%,求a的值.
a%,求a的值. -
科目: 来源: 题型:
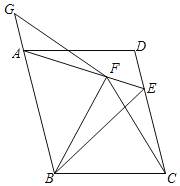
查看答案和解析>>【题目】在平行四边形ABCD中,以AB为边作等边△ABE,点E在CD上,以BC为边作等边△BCF,点F在AE上,点G在BA延长线上且FG=FB.
(1)若CD=6,AF=3,求△ABF的面积;
(2)求证:BE=AG+CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】初中数学代数知识中,方程、函数、不等式存在着紧密的联系,请阅读下列两则材料,回答问题:
利用函数图象找方程
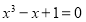 解的范围.设函数
解的范围.设函数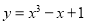 ,当
,当 时,
时,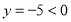 ;当
;当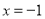 时,
时,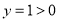 .则函数
.则函数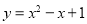 的图象经过两个点
的图象经过两个点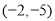 与
与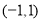 ,而点
,而点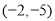 在
在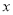 轴下方,点
轴下方,点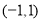 在
在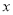 轴上方,则该函数图象与
轴上方,则该函数图象与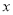 轴交点横坐标必大于-2,小于-1.故,方程
轴交点横坐标必大于-2,小于-1.故,方程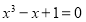 的有解,且该解的范围为
的有解,且该解的范围为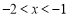 .
.材料二:
解一元二次不等式
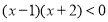 .由“异号两数相乘,结果为负可得:
.由“异号两数相乘,结果为负可得:情况①
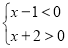 ,得
,得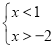 ,则
,则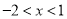
情况②
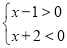 ,得
,得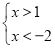 ,则无解
,则无解故,
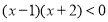 的解集为
的解集为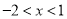 .
.(1)请根据材料一解决问题:已知方程
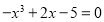 有唯一解
有唯一解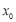 ,且
,且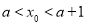 (
(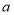 为整数),求整数
为整数),求整数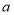 的值.
的值. (2)请结合材料一与材料二解决问题:若关于
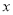 的方程
的方程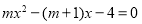 的解分别为
的解分别为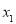 ,
,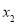 ,且
,且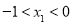 ,
,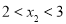 ,求
,求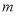 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】边长为4、中心为
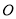 的正方形
的正方形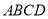 如图所示,动点
如图所示,动点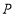 从点
从点 出发,沿
出发,沿 以每秒1个单位长度的速度运动到点
以每秒1个单位长度的速度运动到点 时停止,动点
时停止,动点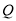 从点
从点 出发,沿
出发,沿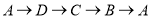 以每秒2个单位长度的速度运动一周停止,若点
以每秒2个单位长度的速度运动一周停止,若点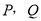 同时开始运动,点
同时开始运动,点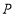 的运动时间为
的运动时间为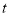
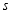 ,当
,当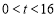 时,满足
时,满足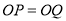 的点
的点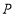 的位置有( )
的位置有( )
A.6个B.7个C.8个D.9个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
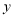 关于
关于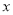 的二次函数
的二次函数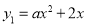 和一次函数
和一次函数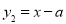 ,若函数
,若函数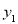 的图象始终在函数
的图象始终在函数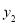 的图象的一侧,则常数
的图象的一侧,则常数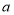 的取值范围是__________.
的取值范围是__________. -
科目: 来源: 题型:
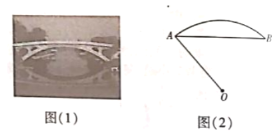
查看答案和解析>>【题目】1400多年前,我国隋代建造的石拱桥——赵州桥(如图(1)),是我国古代人民勤劳与智慧的结晶.如图(2)是它的简化示意图,主桥拱是
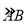 ,拱高(
,拱高(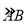 的中点到弦
的中点到弦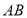 的距离)为
的距离)为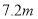 .
. 
(1)在图(2)中(点
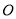 为圆心),用尺规作图作出
为圆心),用尺规作图作出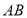 的中点
的中点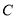 .(不要求写作法,但保留作图痕迹)
.(不要求写作法,但保留作图痕迹)(2)若
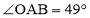 ,求主桥拱的跨度
,求主桥拱的跨度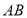 的长.(结果精确到
的长.(结果精确到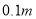 参考数据:
参考数据: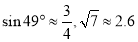 )
)
相关试题

