【题目】如图,![]() 是直线
是直线![]() 上的一点,射线
上的一点,射线![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() .
.
(1)与![]() 相等的角有_____________;
相等的角有_____________;
(2)与![]() 互余的角有______________;
互余的角有______________;
(3)已知![]() ,求
,求![]() 的度数.
的度数.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 、
、![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据角平分线的性质可得与∠COD相等的角;
(2)根据等角的余角相等可得与∠AOC互余的角有∠BOE,∠DOE;
(3)根据余角的定义计算即可.
解:(1)∵![]() 平分
平分![]() ,
,
∴![]() =
=![]() ,
,
故答案为:![]() ;
;
(2)∵![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() ,
,
∴∠COD=∠AOC=![]() ∠AOD,∠DOE=∠BOE=
∠AOD,∠DOE=∠BOE=![]() ∠BOD,
∠BOD,
∵∠AOB=∠AOD+∠BOD=180°,
∴![]() (∠AOD+∠BOD)=90°,
(∠AOD+∠BOD)=90°,
则有∠AOC+∠DOE=90°,∠AOC+∠BOE=90°,
∴与![]() 互余的角有∠DOE,∠BOE,
互余的角有∠DOE,∠BOE,
故答案为:![]() 、
、![]() ;
;
(3)∵![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年5月6日,中国第一条具有自主知识产权的长沙磁浮线正式开通运营,该路线连接了长沙火车南站和黄花国际机场两大交通枢纽,沿线生态绿化带走廊的建设尚在进行中,届时将给乘客带来美的享受.星城渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨,5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
(2)该渣土运输公司决定派出大、小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不少于148吨,且小型渣土运输车至少派出2辆,则有哪几种派车方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP、PC,△BPC是以PB为腰的等腰三角形,则PB的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB = OA=3.(1)、求点A、B的坐标;(2)、已知点C(-2,2),求△BOC的面积;(3)、点P是第一象限角平分线上一点,若
 ,求点P的坐标.
,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料
下面是小明同学“作一个角等于
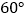 的直角三角形”的尺规作图过程.
的直角三角形”的尺规作图过程.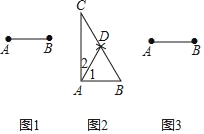
已知:线段
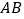 (如图1)
(如图1)求作:
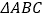 ,使
,使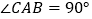 ,
,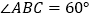 ,
,作法:如图2,
(1)分别以点
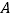 ,点
,点 为圆心,
为圆心,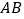 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点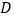 ,连接
,连接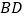
(2)连接
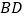 并延长,使得
并延长,使得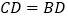 ;
;(3)连接
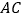
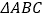 就是所求的直角三角形
就是所求的直角三角形证明:连接
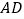 .
.由作图可知,
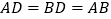 ,
,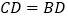
∴
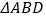 是等边三角形(等边三角形定义)
是等边三角形(等边三角形定义)∴
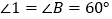 (等边三角形每个内角都等于
(等边三角形每个内角都等于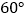 )
)∴
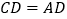
∴
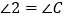 (等边对等角)
(等边对等角)在
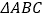 中,
中, (三角形的内角和等于
(三角形的内角和等于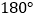 )
)∴
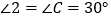
∴
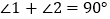 (三角形的内角和等于
(三角形的内角和等于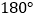 ),即
),即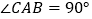 ,
,∴
 就是所求作的直角三角形
就是所求作的直角三角形请你参考小明同学解决问题的方式,利用图3再设计一种“作一个角等于
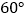 的直角三角形”的尺规作图过程(保留作图痕迹),并写出作法,证明,及推理依据.
的直角三角形”的尺规作图过程(保留作图痕迹),并写出作法,证明,及推理依据. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )

A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程|x-1|+|x+2|=5.由绝对值的几何意义知,该方程表示求在数轴上与1和-2的距离之和为5的点对应的x的值.在数轴上,1和-2的距离为3,满足方程的x对应点在1的右边或-2的左边,若x对应点在1的右边,由图可以看出x=2;同理,若x对应点在-2的左边,可得x=-3,故原方程的解是x=2或x=-3.

参考阅读材料,解答下列问题:
(1)方程|x+3|=4的解为________.
(2)解不等式|x-3|+|x+4|≥9;
(3)若|x-3|+|x+4|≥a对任意的x都成立,求a的取值范围.
相关试题

