【题目】如图,在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP、PC,△BPC是以PB为腰的等腰三角形,则PB的长为 . 
参考答案:
【答案】5或6
【解析】解:如图,
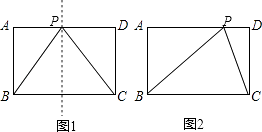
在矩形ABCD中,AB=CD=4,BC=AD=6.
如图1,当PB=PC时,点P是BC的中垂线与AD的交点,则AP=DP= ![]() AD=3.
AD=3.
在Rt△ABP中,由勾股定理得 PB= ![]() =
= ![]() =5;
=5;
如图2,当BP=BC=6时,△BPC也是以PB为腰的等腰三角形.
综上所述,PB的长度是5或6.
所以答案是:5或6.
【考点精析】通过灵活运用等腰三角形的判定和勾股定理的概念,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;(图1)
(2)求∠FAE的度数;(图1)
(3)如图2,延长CF到G点,使BF=GF,连接AG.求证:CD=CG;并猜想CD与2BF+DE的关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】探索:小明在研究数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠C的数量关系.

发现:在如图中,:∠APC=∠A+∠C;如图
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A(_ __)
∵PQ∥AB,AB∥CD.
∴PQ∥CD(__ _)
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
(1)为小明的证明填上推理的依据;
(2)应用:①在如图中,∠P与∠A、∠C的数量关系为__ _;
②在如图中,若∠A=30
 ,∠C=70
,∠C=70 ,则∠P的度数为__ _;
,则∠P的度数为__ _;(3)拓展:在如图中,探究∠P与∠A,∠C的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年5月6日,中国第一条具有自主知识产权的长沙磁浮线正式开通运营,该路线连接了长沙火车南站和黄花国际机场两大交通枢纽,沿线生态绿化带走廊的建设尚在进行中,届时将给乘客带来美的享受.星城渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨,5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
(2)该渣土运输公司决定派出大、小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不少于148吨,且小型渣土运输车至少派出2辆,则有哪几种派车方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB = OA=3.(1)、求点A、B的坐标;(2)、已知点C(-2,2),求△BOC的面积;(3)、点P是第一象限角平分线上一点,若
 ,求点P的坐标.
,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是直线
是直线 上的一点,射线
上的一点,射线 ,
, 分别平分
分别平分 和
和 .
.(1)与
 相等的角有_____________;
相等的角有_____________;(2)与
 互余的角有______________;
互余的角有______________;(3)已知
 ,求
,求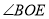 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料
下面是小明同学“作一个角等于
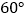 的直角三角形”的尺规作图过程.
的直角三角形”的尺规作图过程.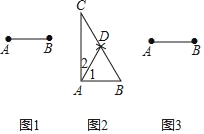
已知:线段
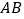 (如图1)
(如图1)求作:
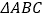 ,使
,使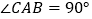 ,
,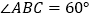 ,
,作法:如图2,
(1)分别以点
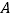 ,点
,点 为圆心,
为圆心,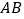 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点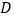 ,连接
,连接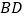
(2)连接
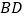 并延长,使得
并延长,使得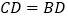 ;
;(3)连接
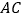
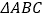 就是所求的直角三角形
就是所求的直角三角形证明:连接
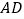 .
.由作图可知,
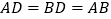 ,
,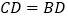
∴
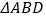 是等边三角形(等边三角形定义)
是等边三角形(等边三角形定义)∴
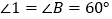 (等边三角形每个内角都等于
(等边三角形每个内角都等于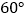 )
)∴
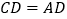
∴
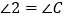 (等边对等角)
(等边对等角)在
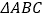 中,
中, (三角形的内角和等于
(三角形的内角和等于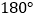 )
)∴
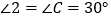
∴
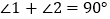 (三角形的内角和等于
(三角形的内角和等于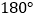 ),即
),即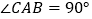 ,
,∴
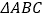 就是所求作的直角三角形
就是所求作的直角三角形请你参考小明同学解决问题的方式,利用图3再设计一种“作一个角等于
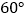 的直角三角形”的尺规作图过程(保留作图痕迹),并写出作法,证明,及推理依据.
的直角三角形”的尺规作图过程(保留作图痕迹),并写出作法,证明,及推理依据.
相关试题

