【题目】阅读下列材料
下面是小明同学“作一个角等于![]() 的直角三角形”的尺规作图过程.
的直角三角形”的尺规作图过程.
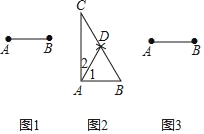
已知:线段![]() (如图1)
(如图1)
求作:![]() ,使
,使![]() ,
,![]() ,
,
作法:如图2,
(1)分别以点![]() ,点
,点![]() 为圆心,
为圆心,![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ,连接
,连接![]()
(2)连接![]() 并延长,使得
并延长,使得![]() ;
;
(3)连接![]()
![]() 就是所求的直角三角形
就是所求的直角三角形
证明:连接![]() .
.
由作图可知,![]() ,
,![]()
∴![]() 是等边三角形(等边三角形定义)
是等边三角形(等边三角形定义)
∴![]() (等边三角形每个内角都等于
(等边三角形每个内角都等于![]() )
)
∴![]()
∴![]() (等边对等角)
(等边对等角)
在![]() 中,
中,![]() (三角形的内角和等于
(三角形的内角和等于![]() )
)
∴![]()
∴![]() (三角形的内角和等于
(三角形的内角和等于![]() ),即
),即![]() ,
,
∴![]() 就是所求作的直角三角形
就是所求作的直角三角形
请你参考小明同学解决问题的方式,利用图3再设计一种“作一个角等于![]() 的直角三角形”的尺规作图过程(保留作图痕迹),并写出作法,证明,及推理依据.
的直角三角形”的尺规作图过程(保留作图痕迹),并写出作法,证明,及推理依据.
参考答案:
【答案】作图见解析,证明见解析.
【解析】
(1)延长![]() 至
至![]() ,使
,使![]() ;(2)分别以点
;(2)分别以点![]() ,点
,点![]() 为圆心,
为圆心,![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ;(3)连接
;(3)连接![]() .根据作图过程,连接CD,得到△DBC是等边三角形,根据等边三角形的性质得到∠B=60°,根据等腰三角形的性质证明即可.
.根据作图过程,连接CD,得到△DBC是等边三角形,根据等边三角形的性质得到∠B=60°,根据等腰三角形的性质证明即可.
作法:(1)延长![]() 至
至![]() ,使
,使![]() ;
;
(2)分别以点![]() ,点
,点![]() 为圆心,
为圆心,![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ;
;
(3)连接![]() .
.
则![]() 就是所求的直角三角形,
就是所求的直角三角形,
证明:连接![]() .
.
由作图可知,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 就是所求作的直角三角形.
就是所求作的直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP、PC,△BPC是以PB为腰的等腰三角形,则PB的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB = OA=3.(1)、求点A、B的坐标;(2)、已知点C(-2,2),求△BOC的面积;(3)、点P是第一象限角平分线上一点,若
 ,求点P的坐标.
,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是直线
是直线 上的一点,射线
上的一点,射线 ,
, 分别平分
分别平分 和
和 .
.(1)与
 相等的角有_____________;
相等的角有_____________;(2)与
 互余的角有______________;
互余的角有______________;(3)已知
 ,求
,求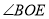 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )

A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程|x-1|+|x+2|=5.由绝对值的几何意义知,该方程表示求在数轴上与1和-2的距离之和为5的点对应的x的值.在数轴上,1和-2的距离为3,满足方程的x对应点在1的右边或-2的左边,若x对应点在1的右边,由图可以看出x=2;同理,若x对应点在-2的左边,可得x=-3,故原方程的解是x=2或x=-3.

参考阅读材料,解答下列问题:
(1)方程|x+3|=4的解为________.
(2)解不等式|x-3|+|x+4|≥9;
(3)若|x-3|+|x+4|≥a对任意的x都成立,求a的取值范围.
-
科目: 来源: 题型:
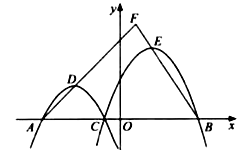
查看答案和解析>>【题目】如图,在平面直角坐标系
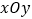 中,已知
中,已知 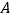 ,
, 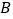 两点的坐标分别为
两点的坐标分别为 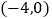 ,
, 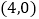 ,
, 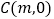 是线段
是线段 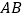 上一点(与
上一点(与 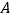 ,
, 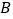 点不重合),抛物线
点不重合),抛物线 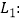
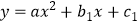 (
(  )经过点
)经过点 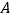 ,
, 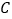 ,顶点为
,顶点为 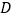 ,抛物线
,抛物线 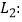
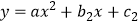 (
(  )经过点
)经过点 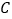 ,
, 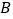 ,顶点为
,顶点为 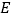 ,
, 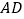 ,
, 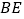 的延长线相交于点
的延长线相交于点  .
.
(1)若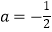 ,
, 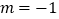 ,求抛物线
,求抛物线 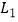 ,
, 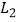 的解析式;
的解析式;
(2)若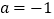 ,
, 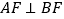 ,求
,求 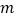 的值;
的值;
(3)是否存在这样的实数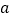 (
(  ),无论
),无论 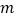 取何值,直线
取何值,直线 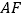 与
与 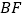 都不可能互相垂直?若存在,请直接写出
都不可能互相垂直?若存在,请直接写出 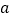 的两个不同的值;若不存在,请说明理由.
的两个不同的值;若不存在,请说明理由.
相关试题

