搜索
【题目】如图，一宽为2cm的刻度尺在圆上移动，当刻度尺的一边与圆相切时，另一边与圆两个交点处的读数恰好为“1”和“4”（单位：cm），则该圆的半径为（ ）
A.5cm
B.
cm
C.
cm
D.
cm
参考答案：
【答案】C
【解析】解：如图所示，连接OA，根据题意知，
PC=2cm，OP⊥AB，
∴AP=BP，
∵AB=3cm，
∴AP=
cm，
在Rt△AOP中，设OA=x，则0P=x﹣2，
根据勾股定理得，
+（x﹣2）2=x2 ，
解得，x=
．
故选C．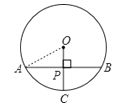
【考点精析】利用勾股定理的概念和垂径定理对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
-
科目： 来源： 题型：
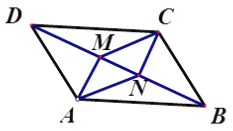
查看答案和解析>>【题目】如图，在平行四边形ABCD中，AM、CN都是BD的垂线，M、N是垂足．
求证：（1）AM=CN；（2）∠MAN=∠NCM．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=
x+6与y轴交于点A，与x轴交于点B，点M是射线AB上一动点（点M不与点A、B重合），以点M为圆心，MA长为半径的圆交y轴于另一点C，直线MC与x轴交于点D，点E是线段BD的中点，射线ME交⊙M于点F，连接OF．
（1）若MA=2，求C点的坐标；
（2）若D点的坐标为（4，0），求MC的长；
（3）当OF=MA时，直接写出点M的坐标．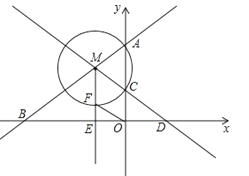
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把一根绳子对折成线段AB，从点P处把绳子剪断，已知AP：BP＝2：3，若剪断后的各段绳子中最长的一段为60 cm，求绳子的原长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知O为直线AB上一点，∠COE是直角，OF平分∠AOE.
(1)如图①，若∠COF＝34°，则∠BOE＝________；若∠COF＝n°，则∠BOE＝________；∠BOE与∠COF的数量关系为________________．
(2)当射线OE绕点O逆时针旋转到如图②的位置时，(1)中∠BOE与∠COF的数量关系是否仍然成立？请说明理由．
(3)在图③中，若∠COF＝65°，在∠BOE的内部是否存在一条射线OD，使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半？若存在，请求出∠BOD的度数；若不存在，请说明理由．
-
科目： 来源： 题型：
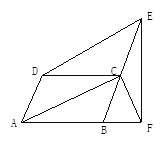
查看答案和解析>>【题目】如图，四边形ABCD是平行四边形，DE//AC，交BC的延长线于点E，EF⊥AB于点F.求证：（1）BC=CE；（2）AD=CF.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，对角线AC、BD交于点O，BE平分∠ABC交AC于点F，交AD于点E，且∠DBF=15°，求证：（1）AO=AE; (2)∠FEO的度数.
相关试题
