【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发以每秒1cm的速度向点C运动,设运动时间为t秒(t>0).
(1)若点P恰好在∠ABC的角平分线上,求出此时t的值;
(2)若点P使得PB+PC=AC时,求出此时t的值.

参考答案:
【答案】(1)5;(2)![]()
【解析】
(1)作PD⊥AB于D,如图,AP=t,先利用勾股定理计算出AC=8,再根据角平分线的性质得到PC=PD=8-t,利用三角形面积公式得到![]() ×10×(8-t)+
×10×(8-t)+![]() ×6×(8-t)=
×6×(8-t)=![]() ×6×8,然后解方程即可;
×6×8,然后解方程即可;
(2)先证明PB=PA=t,再利用勾股定理得到(8-t)2+62=t2,然后解方程即可.
(1)作PD⊥AB于D,如图,AP=t,
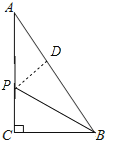
∵∠ACB=90°,AB=10,BC=6,
∴AC=![]() ,
,
∵BP平分∠ABC,
∴PC=PD=8-t,
∵S△ABP+S△BCP=S△ABC,
∴![]() ×10×(8-t)+
×10×(8-t)+![]() ×6×(8-t)=
×6×(8-t)=![]() ×6×8,
×6×8,
解得t=5,
即此时t的值为5;
(2)∵PB+PC=AC,PA+PC=AC,
∴PB=PA=t,
在Rt△BCP中,∵PC2+BC2=BP2,
∴(8-t)2+62=t2,解得t=![]() ,
,
即此时t的值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备
 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.A型
B型
价格
 万元
万元 台
台
a
b
处理污水量
 吨
吨 月
月
240
200
 求a,b的值;
求a,b的值;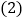 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案; 在
在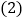 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点
 的坐标为
的坐标为 ,将点
,将点 向右平移
向右平移 个单位得到点
个单位得到点 ,其中关于
,其中关于 的一元一次不等式
的一元一次不等式 的解集为
的解集为 ,过点
,过点 作
作 轴于
轴于 .
.(1)求
 两点坐标及四边形
两点坐标及四边形 的面积;
的面积;(2)如图2,点
 自
自 点以1个单位/秒的速度在
点以1个单位/秒的速度在 轴上向上运动,点
轴上向上运动,点 自
自 点以2个单位/秒的速度在
点以2个单位/秒的速度在 轴上向左运动,设运动时间为
轴上向左运动,设运动时间为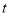 秒(
秒( ),是否存在一段时间使得
),是否存在一段时间使得 ,若存在,求出
,若存在,求出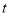 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;(3)在(2)的条件下,求四边形
 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处B.二处C.三处D.四处
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,点 E,F,G 分别在 BC,AC,AB 上,AE 与 BF 交于点 O,且点 O 在 CG 上,根据尺规作图的痕迹,判断下列说法不正确的是( )

A.AE,BF 是△ABC 的角平分线B.点 O 到△ABC 三边的距离相等
C.CG 也是△ABC 的一条角平分线D.AO=BO=CO
-
科目: 来源: 题型:
查看答案和解析>>【题目】设中学生体质健康综合评定成绩为
 分,满分为100分,规定:
分,满分为100分,规定: 为
为 级,
级, 为
为 级,
级, 为
为 级,
级, 为
为 级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
(1)在这次调查中,一共抽取了__________名学生;
(2)扇形统计图中,
 ________%,
________%, 级对应的圆心角为______度;
级对应的圆心角为______度;(3)若该中学共有学生1200名,请你利用你所学的统计知识,估计综合评定成绩为
 级的学生有多少名?
级的学生有多少名?
相关试题

