【题目】如图,在等边三角形ABC中,BD是AC边上的中线,延长BC到E,使CE=CD.
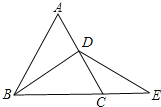
问:
(1)DB与DE相等吗?
(2)把BD是AC边上的中线改成什么条件,还能得到同样的结论?
参考答案:
【答案】(1)相等,理由见解析;(2)把BD是AC边上的中线改为BD是∠ABC的平分线或BD是AC边上的高,根据等边三角形“三线合一”的性质,还能得出DB=DE.
【解析】
试题分析:(1)由CD=CE,得到∠E=∠EDC,由于∠ACB=60°,求得∠E=30°,于是得到∠E=∠DBC,根据等腰三角形的判定即可得到结论;
(2)根据等边三角形“三线合一”的性质,即可得到结论.
解:(1)相等,
理由:∵CD=CE,
∴∠E=∠EDC,
又∵∠ACB=60°,
∴∠E=30°,
又∵∠DBC=30°,
∴∠E=∠DBC,
∴DB=DE;
(2)把BD是AC边上的中线改为BD是∠ABC的平分线或BD是AC边上的高,根据等边三角形“三线合一”的性质,还能得出DB=DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数的平方根是2a-1与-a+2,求a和这个正数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为5cm,点A为线段OP的中点,当OP=11cm时,点A和⊙O的位置关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是等边△ABC边AB上的一点,且AD=1,BD=2,现将△ABC折叠,使点C与D重合,折痕EF,点E、F分别在AC和BC上,若BF=1.2,则CE=( )
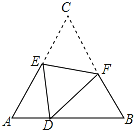
A.
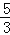 B.
B.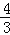 C.
C.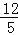 D.
D.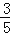
-
科目: 来源: 题型:
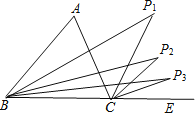
查看答案和解析>>【题目】如图,已知∠A=n°,若P1点是∠ABC和外角∠ACE的角平分线的交点,P2点是∠P1BC和外角∠P1CE的角平分线的交点,P3点是∠P2BC和外角∠P2CE的交点…依此类推,则∠Pn=( )
A.
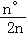 B.
B.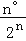 C.
C.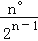 D.
D.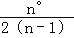
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+2)(2x-n)=2x2+mx-2,则( )
A. m=3,n=1; B. m=5,n=1; C. m=3,n=-1; D. m=5,n=-1;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是一元二次方程x2+mx+n=0的一个根,则m2+2mn+n2的值为 .
相关试题

