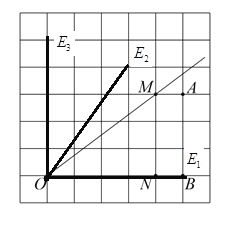
【题目】如图,是由49个边长为1的小正方形组成的7×7的正方形网格,小正方形的顶点为格点,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均在格点上.
均在格点上.

(1)直接写出![]() ________;
________;
(2)点![]() 在网格中的格点上,且
在网格中的格点上,且![]() 是以
是以![]() 为顶角顶点的等腰三角形,则满足条件的点
为顶角顶点的等腰三角形,则满足条件的点![]() 有________个;
有________个;
(3)请在如图所示的网格中,借助矩形![]() 和无刻度的直尺作出
和无刻度的直尺作出![]() 的角平分线,并保留作图痕迹.
的角平分线,并保留作图痕迹.
参考答案:
【答案】(1)5;(2)3;(3)详见解析
【解析】
(1)利用勾股定理直接得到答案,
(2)由![]() 得
得![]() 在网格中找到点
在网格中找到点![]() 即可,
即可,
(3)如图,连接![]() 交于点
交于点![]() ,可证明
,可证明![]() 是
是![]() 的角平分线.
的角平分线.
解:(1)由勾股定理得:![]()
故答案为:![]()
(2)如图,由![]()
![]()
所以满足条件的点![]() 有3个.
有3个.
故答案为:![]()
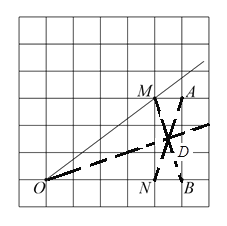
(3)如图,连接![]() 交于点
交于点![]() ,连接
,连接![]()
则![]() 是
是![]() 的角平分线,
的角平分线,
理由如下:
![]() 矩形
矩形![]()
![]()
![]()
![]()
![]()
![]()
![]() 是
是![]() 的角平分线.
的角平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=
 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.(1)求函数y=kx+b和y=
 的表达式;
的表达式;(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据:
 ,结果保留整数.)
,结果保留整数.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,… 组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒
 个单位长度,则第2019秒时,点P的坐标是________________
个单位长度,则第2019秒时,点P的坐标是________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣4x+5.
(1)将y=x2﹣4x+5化成y=a (x﹣h)2+k的形式;
(2)指出该二次函数图象的对称轴和顶点坐标;
(3)当x取何值时,y随x的增大而增大?
-
科目: 来源: 题型:
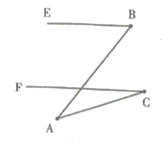
查看答案和解析>>【题目】如图(a),木杆EB与FC平行,木杆的两端B,C用一橡皮筋连接,现将图(a)中的橡皮筋拉成下列各图的形状,试解答下列各题:

(1)探究图(b)、(c)、(d)、(e)中,
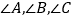 之间的数量关系,并填空;
之间的数量关系,并填空;①图(b)中,
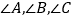 之间的关系是________________________;
之间的关系是________________________;②图(c)中,
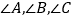 之间的关系是_________________________;
之间的关系是_________________________;③图(d)中,
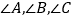 之间的关系是__________________________;
之间的关系是__________________________;④图(e)中,
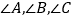 之间的关系是__________________________;
之间的关系是__________________________;(2)探究图(f)、(g)中,
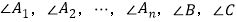 之间的数量关系,并填空:
之间的数量关系,并填空:①图(f)中,
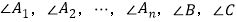 之间的关系是________________________________;
之间的关系是________________________________;②图(g)中,
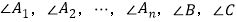 之间的关系是________________________________;
之间的关系是________________________________;(3)请对图(e)的结论加以证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)
(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′B′C′的坐标;
(3)求△ABC的面积.

相关试题

