【题目】将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )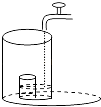
A.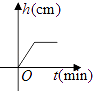
B.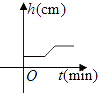
C.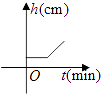
D.
参考答案:
【答案】B
【解析】将一盛有部分水的圆柱形小玻璃杯放入事先没有水的大圆柱形容器内,小玻璃杯内的水原来的高度一定大于0,则可以判断A、D一定错误,用一注水管沿大容器内壁匀速注水,水开始时不会流入小玻璃杯,因而这段时间h不变,当大杯中的水面与小杯水平时,开始向小杯中流水,h随t的增大而增大,当水注满小杯后,小杯内水面的高度h不再变化.
所以答案是:B.
【考点精析】本题主要考查了函数的图象的相关知识点,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.已知,
 中,
中, ,
, ,点
,点 、
、 在边
在边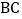 上,且
上,且 .
.
(1)如图
 ,当
,当 时,将
时,将 绕点
绕点 顺时针旋转
顺时针旋转 到
到 的位置,连接
的位置,连接 ,
,①求
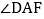 的度数;
的度数;②求证:
 ;
;(2)如图
 ,当
,当 时,猜想
时,猜想 、
、 、
、 的数量关系,并说明理由;
的数量关系,并说明理由;(3)如图
 ,当
,当 ,
, ,
, 时,请直接写出
时,请直接写出 的长为________.
的长为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(﹣2,0),C(0,4),点O′为x轴上一点,⊙O′过A,C两点交x轴于另一点B.

(1)求点O′的坐标;
(2)已知抛物线y=ax2+bx+c过A,B,C三点,且与⊙O′交于另一点E,求抛物线的解析式,并直接写出点E 坐标;
(3)设点P(t,0)是线段OB上一个动点,过点P作直线l⊥x轴,交线段BC于F,交抛物线y=ax2+bx+c于点G,请用t表示四边形BPCG的面积S;
(4)在(3)的条件下,四边形BPCG能否为平行四边形?若能,请求出t的值;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B在数轴上分别表示a,b.
(1)对照数轴填写下表:
a
6
-6
-6
-6
2
-1.5
b
4
0
4
-4
-10
-1.5
A、B两点的距离
(2)若A、B两点间的距离记为d,试问:d和a,b有何数量关系?
(3)在数轴上找出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求所有这些整数的和;
(4)若点C表示的数为x,当点C在什么位置时,
 取得的值最小? 最小值是多少?
取得的值最小? 最小值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:
①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE
 S菱形ABCD
S菱形ABCD下列判断正确的是( )

A. ①,②都对B. ①,②都错C. ①对,②错D. ①错,②对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2AD,点E,F分别是AB,BC边的中点,连接AF,CE交于点M,连接BM并延长交CD于点N,连接DE交AF于点P,则结论:①∠ABN=∠CBN;②DE∥BN;③△CDE是等腰三角形;④EM:BE=
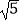 :3;⑤S△EPM=
:3;⑤S△EPM=  S梯形ABCD , 正确的个数有( )
S梯形ABCD , 正确的个数有( )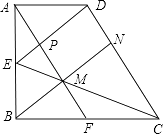
A.5个
B.4个
C.3个
D.2个 -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰长为5,一边上的高为3,则底边长为 .
相关试题

