【题目】如图,在平面直角坐标系中,已知A(﹣2,0),C(0,4),点O′为x轴上一点,⊙O′过A,C两点交x轴于另一点B.
(1)求点O′的坐标;
(2)已知抛物线y=ax2+bx+c过A,B,C三点,且与⊙O′交于另一点E,求抛物线的解析式,并直接写出点E 坐标;
(3)设点P(t,0)是线段OB上一个动点,过点P作直线l⊥x轴,交线段BC于F,交抛物线y=ax2+bx+c于点G,请用t表示四边形BPCG的面积S;
(4)在(3)的条件下,四边形BPCG能否为平行四边形?若能,请求出t的值;若不能,请说明理由.
参考答案:
【答案】
(1)解:如图1中,连接CO′,设⊙O′的半径为R.

在Rt△OCO′中,∵OC2+OO2=CO′2,
∴42+(R﹣2)2=R2,
∴R=5,
∴OO′=5﹣2=3,
∴O′(3,0).
(2)解:∵A(﹣2,0),C(0,4),B(8,0),
∴  ,解得
,解得 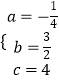 ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+4.
x+4.
易知E、C关于对称轴对称,
∴点E的纵坐标为4,
∴E(6,4)
(3)解:由题意G(t,﹣ ![]() t2+
t2+ ![]() t+4),
t+4),
∴S四边形BPCG= ![]() PG(Bx﹣Cx)=
PG(Bx﹣Cx)= ![]() (﹣
(﹣ ![]() t2+
t2+ ![]() t+4)8=﹣t2+6t+16(0<t<8)
t+4)8=﹣t2+6t+16(0<t<8)
(4)解:不可能是平行四边形.
理由:假设CG∥BP,此时G与E重合,CE=OP=6,BP=OB﹣OP=2,
∴CE≠BP,
∴四边形BPCG不可能是平行四边形.
【解析】(1)如图1中,连接CO′,设⊙O′的半径为R.在Rt△OCO′中,根据OC2+OO2=CO′2,可得42+(R-2)2=R2,解方程求出求点O′的坐标;
(2)把A(-2,0),C(0,4),B(8,0)代入抛物线抛物线y=ax2+bx+c,求抛物线的解析式即点E 坐标;
(3)根据S四边形BPCG=![]() PG(Bx-Cx),即可用t表示四边形BPCG的面积S
PG(Bx-Cx),即可用t表示四边形BPCG的面积S
(4)不可能是平行四边形.假设CG∥BP,此时G与E重合,CE=OP=6,BP=OB-OP=2,推出CE≠BP,即可得到所求结论..
【考点精析】本题主要考查了勾股定理的概念和平行四边形的判定与性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2015,则m的值是( )
A.43B.44C.45D.46
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”黄金周,坚胜家电城大力促销,收银情况一直看好
 下表为当天与前一天的营业额的涨跌情况
下表为当天与前一天的营业额的涨跌情况 已知9月30日的营业额为26万元.
已知9月30日的营业额为26万元.10月1日
2日
3日
4日
5日
6日
7日
4
3
2
0



 黄金周内收入最低的哪一天?
黄金周内收入最低的哪一天? 直接回答,不必写过程
直接回答,不必写过程 .
. 黄金周内平均每天的营业额是多少?
黄金周内平均每天的营业额是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.已知,
 中,
中, ,
, ,点
,点 、
、 在边
在边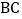 上,且
上,且 .
.
(1)如图
 ,当
,当 时,将
时,将 绕点
绕点 顺时针旋转
顺时针旋转 到
到 的位置,连接
的位置,连接 ,
,①求
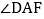 的度数;
的度数;②求证:
 ;
;(2)如图
 ,当
,当 时,猜想
时,猜想 、
、 、
、 的数量关系,并说明理由;
的数量关系,并说明理由;(3)如图
 ,当
,当 ,
, ,
, 时,请直接写出
时,请直接写出 的长为________.
的长为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B在数轴上分别表示a,b.
(1)对照数轴填写下表:
a
6
-6
-6
-6
2
-1.5
b
4
0
4
-4
-10
-1.5
A、B两点的距离
(2)若A、B两点间的距离记为d,试问:d和a,b有何数量关系?
(3)在数轴上找出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求所有这些整数的和;
(4)若点C表示的数为x,当点C在什么位置时,
 取得的值最小? 最小值是多少?
取得的值最小? 最小值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )
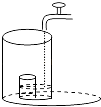
A.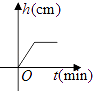
B.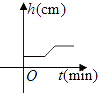
C.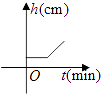
D.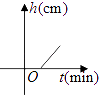
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:
①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE
 S菱形ABCD
S菱形ABCD下列判断正确的是( )

A. ①,②都对B. ①,②都错C. ①对,②错D. ①错,②对
相关试题

