【题目】如图,已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2AD,点E,F分别是AB,BC边的中点,连接AF,CE交于点M,连接BM并延长交CD于点N,连接DE交AF于点P,则结论:①∠ABN=∠CBN;②DE∥BN;③△CDE是等腰三角形;④EM:BE= ![]() :3;⑤S△EPM=
:3;⑤S△EPM= ![]() S梯形ABCD , 正确的个数有( )
S梯形ABCD , 正确的个数有( )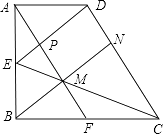
A.5个
B.4个
C.3个
D.2个
参考答案:
【答案】B
【解析】连接DF,AC,EF,如图所示:
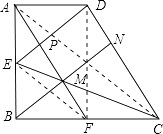
∵E、F分别为AB、BC的中点,且AB=BC,
∴AE=EB=BF=FC,
在△ABF和△CBE中,
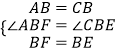 ,
,
∴△ABF≌△CBE(SAS),
∴∠BAF=∠BCE,AF=CE,
在△AME和△CMF中,
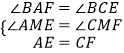 ,
,
∴△AME≌△CMF(AAS),
∴EM=FM,
在△BEM和△BFM中,
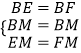 ,
,
∴△BEM≌△BFM(SSS),
∴∠ABN=∠CBN,选项①正确;
∵AE=AD,∠EAD=90°,
∴△AED为等腰直角三角形,
∴∠AED=45°,
∵∠ABC=90°,
∴∠ABN=∠CBN=45°,
∴∠AED=∠ABN=45°,
∴ED∥BN,选项②正确;
∵AB=BC=2AD,且BC=2FC,
∴AD=FC,又AD∥FC,
∴四边形AFCD为平行四边形,
∴AF=DC,又AF=CE,
∴DC=EC,
则△CED为等腰三角形,选项③正确;
∵EF为△ABC的中位线,
∴EF∥AC,且EF= ![]() AC,
AC,
∴∠MEF=∠MCA,∠EFM=∠MAC,
∴△EFM∽△CAM,
∴EM:MC=EF:AC=1:2,
设EM=x,则有MC=2x,EC=EM+MC=3x,
设EB=y,则有BC=2y,
在Rt△EBC中,根据勾股定理得:EC= ![]() =
= ![]() y,
y,
∴3x= ![]() y,即x:y=
y,即x:y= ![]() :3,
:3,
∴EM:BE= ![]() :3,选项④正确;
:3,选项④正确;
∵E为AB的中点,EP∥BM,
∴P为AM的中点,
∴S△AEP=S△EPM= ![]() S△AEM,
S△AEM,
又S△AEM=S△BEM,且S△BEM=S△BFM,
∴S△AEM=S△BEM=S△BFM= ![]() S△ABF,
S△ABF,
∵四边形ABFD为矩形,
∴S△ABF=S△ADF,又S△ADF=S△DFC,
∴S△ABF=S△ADF=S△DFC= ![]() S梯形ABCD,
S梯形ABCD,
∴S△EPM= ![]() S梯形ABCD,选项⑤错误.
S梯形ABCD,选项⑤错误.
则正确的个数有4个.
故答案为:B.
连接DF,AC,EF,如图所示,由E、F分别为AB、BC的中点,且AB=BC,得到EB=FB,再由一对公共角相等,利用“SAS”可得出△ABF与△CBE全等,利用AAS可得出△AME与△CMF全等,由全等三角形的对应边相等可得出ME=MF,再由BE=BF,BM=BM,利用SSS得到△BEM与△BFM全等,根据全等三角形的对应角相等可得出∠ABN=∠CBN,选项①正确;由AD=AE,梯形为直角梯形,得到∠EAD为直角,可得出△AED为等腰直角三角形,可得出∠AED为45°,由∠ABC为直角,且∠ABN=∠CBN,可得出∠ABN为45°,根据同位角相等可得出DE平行于BN,选项②正确;先得到AD=FC,又AD与FC平行,得到ADCF为平行四边形,可得出AF=DC,又AF=CE,等量代换可得出DC=EC,即△DCE为等腰三角形,选项③正确;由EF为△ABC的中位线,得出△EFM与△ACM相似,进而可得出EM:MC=1:2,设EM=x,则有MC=2x,用EM+MC表示出EC,设EB=y,根据BC=2EB,表示出BC,在直角三角形BCE中,利用勾股定理表示出EC,两者相等得到x与y的比值,即为EM与BE的比值,即可判断选项④正确与否;由E为AB的中点,利用等底同高得到△AME的面积与△BME的面积相等,由△BME与△BFM全等,得到面积相等,可得出三个三角形的面积相等都为△ABF面积的![]() ,进一步可得出△AEP的面积等于△PEM的面积,得到△PEM的面积为△ABF面积的
,进一步可得出△AEP的面积等于△PEM的面积,得到△PEM的面积为△ABF面积的![]() ,由ABFD为矩形得到△ABF与△ADF全等,面积相等,由△ADF与△CFD全等得到面积相等,可得出三个三角形面积相等都为梯形面积的
,由ABFD为矩形得到△ABF与△ADF全等,面积相等,由△ADF与△CFD全等得到面积相等,可得出三个三角形面积相等都为梯形面积的![]() ,综上得到△PEM的面积为梯形面积的
,综上得到△PEM的面积为梯形面积的![]() ,可得出选项⑤错误,综上,即可得到所求正确的个数.
,可得出选项⑤错误,综上,即可得到所求正确的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B在数轴上分别表示a,b.
(1)对照数轴填写下表:
a
6
-6
-6
-6
2
-1.5
b
4
0
4
-4
-10
-1.5
A、B两点的距离
(2)若A、B两点间的距离记为d,试问:d和a,b有何数量关系?
(3)在数轴上找出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求所有这些整数的和;
(4)若点C表示的数为x,当点C在什么位置时,
 取得的值最小? 最小值是多少?
取得的值最小? 最小值是多少? -
科目: 来源: 题型:
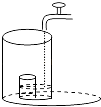
查看答案和解析>>【题目】将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )
A.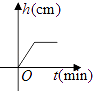
B.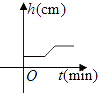
C.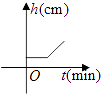
D.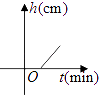
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:
①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE
 S菱形ABCD
S菱形ABCD下列判断正确的是( )

A. ①,②都对B. ①,②都错C. ①对,②错D. ①错,②对
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰长为5,一边上的高为3,则底边长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2 , 以AD2为一边,做第二个菱形AB2C2D2 , 使∠B2=60°;作AD3⊥B2C2于点D3 , 以AD3为一边做第三个菱形AB3C3D3 , 使∠B3=60°…依此类推,这样做的第n个菱形ABnCnDn的边ADn的长是 .
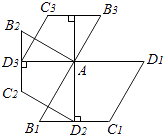
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:

(1)将△ABC向右平移3个单位长度再向下平移2个单位长度,画出两次平移后的△A1B1C1;
(2)写出A1、C1的坐标;
(3)将△A1B1C1绕C1逆时针旋转90°,画出旋转后的△A2B2C1 , 求△A1B1C1旋转过程中扫过的面积(结果保留π)
相关试题

