【题目】在平面内正方形ABCD与正方形CEFH如图放置,连DE,BH,两线交于M.求证: 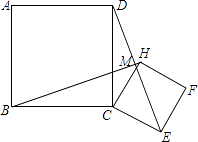
(1)BH=DE.
(2)BH⊥DE.
参考答案:
【答案】
(1)证明:在正方形ABCD与正方形CEFH中,
BC=CD,CE=CH,∠BCD=∠ECH=90°,
∴∠BCD+∠DCH=∠ECH+∠DCH,
即∠BCH=∠DCE,
在△BCH和△DCE中,
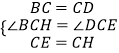 ,
,
∴△BCH≌△DCE(SAS),
∴BH=DE
(2)证明:∵△BCH≌△DCE,
∴∠CBH=∠CDE,
又∵∠CGB=∠MGD,
∴∠DMB=∠BCD=90°,
∴BH⊥DE.
【解析】(1)根据正方形的性质可得BC=CD,CE=CH,∠BCD=∠ECH=90°,然后求出∠BCH=∠DCE,再利用“边角边”证明△BCH和△DCE全等,根据全等三角形对应边相等证明即可;(2)根据全等三角形对应角相等可得∠CBH=∠CDE,然后根据三角形的内角和定理求出∠DMB=∠BCD=90°,再根据垂直的定义证明即可.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式:
(1)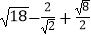 +(
+( 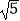 ﹣1)0;
﹣1)0;
(2)a2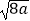 +3a
+3a 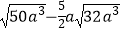 .
. -
科目: 来源: 题型:
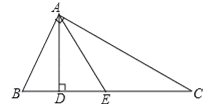
查看答案和解析>>【题目】如图,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.求:
(1)△ABC的面积;
(2)AD的长;
(3)△ACE和△ABE的周长的差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长都是1,
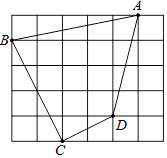
(1)求四边形ABCD的周长和面积;
(2)∠BCD是直角吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】王大伯有甲、乙、丙三块不同等级的棉田60亩、20亩、10亩,想估算自己今年的棉花产量,请你给王大伯出个主意( )
A.从甲棉田抽出部分进行估算
B.从乙棉田抽出部分进行估算
C.从丙棉田抽出部分进行估算
D.按6:2:1的比例从甲、乙、丙三块棉田抽取进行估算 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】要想统计“本班学生最喜欢的动画片”,下列收集数据的方法比较合适的是( )
A.调查问卷
B.访问
C.观察
D.查阅资料
相关试题

