Question

【题目】如图，在△ABC中，OA=8，OB=6，C点与A点关于直线OB对称，动点P、Q分别在线段AC、AB上（点P不与点A．C重合），满足∠BPQ=∠BAO．

（1）当OP=_______时，△APQ≌△CBP，说明理由；

（2）当△PQB为等腰三角形时，求OP的长度．

Answer 1

【答案】（1）2，理由见解析；（2）OP2或．

【解析】

（1）求出∠PAQ=∠BCP，∠AQP=∠BPC，根据点的坐标求出AP=BC，根据全等三角形的判定推出即可．
（2）分为三种情况：①PQ=BP，②BQ=QP，③BQ=BP，根据（2）即可推出①，根据三角形外角性质即可判断②，根据勾股定理得出方程，即可求出③．

解：（1）当OP=2时，△APQ≌△CBP．

理由如下：

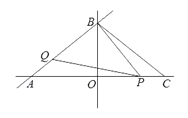
∵OA=8，OB=6，C点与A点关于直线OB对称，

∴，

∵OA=8，OP=2，

∴AP=BC=10

∵C点与A点关于直线OB对称，

∴∠BAO=∠BCO

∵∠BPQ=∠BAO，

∴∠BPQ=∠BCO

∵∠APB=∠APQ+∠BPQ=∠BCO+∠CBP，

∴∠APQ=∠CBP

在△APQ和△CBP中

，

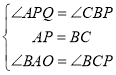∴△APQ≌△CBP（ASA）

（2）分为3种情况：

①当PB=PQ时，

由（1）得：△APQ≌△CBP时，PB=PQ此时OP=2；

②当BQ=BP时，

∠BPQ=∠BQP

∵∠BPQ=∠BAO，

∴∠BAO=∠BQP

根据三角形外角性质得：∠BQP＞∠BAO，

∴这种情况不存在；

③当QB=QP时，

∠QBP=∠BPQ=∠BAO，

∴PB=PA，

设OP=x，则PB=PA=x+8

在Rt△OBP中，PB2=OP2+OB2，

∴（8+x）2=x2+62

解得：x；

∵点P在AC上，

∴点P在点O左边，

此时OP；

∴当△PQB为等腰三角形时，OP2或；