【题目】在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)求证:∠AEB=∠ACF;
(2)求证:EF2BF22AC2.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据等腰三角形的性质得出∠BAF=∠CAF,根据SAS推出△BAF≌△CAF,根据全等得出∠ABF=∠ACF,即可得出答案;
(2)根据全等得出BF=CF,求出∠CFG=∠EAG=90°,根据勾股定理求出EF2+BF2=EF2+CF2=EC2,EC2=AC2+AE2=2AC2,即可得出答案.
(1)证明:如图,

∵AB=AC,D是BC的中点,
∴∠BAF=∠CAF
在△BAF和△CAF中

∴△BAF≌△CAF(SAS),
∴∠ABF=∠ACF
∵AB=AC,△ACE是等腰直角三角形,
∴AB=AE,
∴∠ABE=∠AEB,
∴∠AEB=∠ACF;
(2)证明:∵△BAF≌△CAF,
∴BF=CF
∵∠AGF=∠AEB+∠EAG
∠AGF=∠ACF+∠CFG且∠AEB=∠ACF,
∴∠CFG=∠EAG=90°,
∴EF+BF=EF+CF=EC
∵△ACE是等腰直角三角形,
∴∠CAE=90°,AC=AE,
∴EC2=AC+AE=2AC
即EF+BF=2AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学实验室:

制作4张全等的直角三角形纸片(如图1),把这4张纸片拼成以弦长c为边长的正方形构成“弦图”(如图2),古代数学家利用“弦图”验证了勾股定理.
探索研究:
(1)小明将“弦图”中的2个三角形进行了运动变换,得到图3,请利用图3证明勾股定理;
数学思考:
(2)小芳认为用其它的方法改变“弦图”中某些三角形的位置,也可以证明勾股定理.请你想一种方法支持她的观点(先在备用图中补全图形,再予以证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①两条直线相交,一个角的两邻补角相等,则这两条直线垂直;②同位角相等;③点(5,6)与点(6,5)表示同一点;④若两个同旁内角互补,则它们的角平分线互相垂直;⑤点(
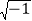 ,5)在第二象限.其中假命题的个数为( )
,5)在第二象限.其中假命题的个数为( )A. 4B. 3C. 2D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】代数式ax2+bx+c(a≠0,a,b,c是常数)中,x与ax2+bx+c的对应值如下表:
x
﹣1
﹣

0

1

2

3
ax2+bx+c
﹣2
﹣

1

2

1
﹣

﹣2
请判断一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1 , x2的取值范围是下列选项中的( )
A.﹣ <x1<0,
<x1<0,  <x2<2
<x2<2
B.﹣1<x1<﹣ ,2<x2<
,2<x2< 
C.﹣ <x1<0,2<x2<
<x1<0,2<x2< 
D.﹣1<x1<﹣ ,
,  <x2<2
<x2<2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
A. ∠E=∠FB. ∠E+∠F=180°
C. 3∠E+∠F=360°D. 2∠E-∠F=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,OA=8,OB=6,C点与A点关于直线OB对称,动点P、Q分别在线段AC、AB上(点P不与点A.C重合),满足∠BPQ=∠BAO.
(1)当OP=_______时,△APQ≌△CBP,说明理由;
(2)当△PQB为等腰三角形时,求OP的长度.

相关试题

