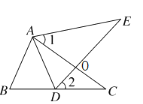
【题目】如图,在△ABC中,点D在线段BC上,∠1=∠2,AE=AC.
(1)在不添加任何字母的情况下,请再补充一个条件,使得△ABC≌△ADE,你补充的条件是 (至少写出两个可行的条件);
(2)请你从所给条件中选一个,使△ABC≌△ADE,并证明.
参考答案:
【答案】(1)∠B=∠ADE;BC=DE;(2)见解析.
【解析】
(1)利用全等三角形的判定定理进一步得出答案即可;
(2)从(1)中选取一个条件,根据全等三角形判定定理进一步证明即可.
(1)∵∠1=∠2,
∴∠E+∠AOE=∠C+COD,
∵∠AOE=∠COD,
∴∠E=∠C,
又∵AE=AC,
∴当∠B=∠ADE时,△ABC≌△ADE(AAS);
当BC=DE时,△ABC≌△ADE(SAS);
故答案为:∠B=∠ADE;BC=DE;
(2)证明当∠B=∠ADE时,△ABC≌△ADE,理由如下:
∵∠1=∠2,
∴∠E+∠AOE=∠C+COD,
∵∠AOE=∠COD,
∴∠E=∠C,
在△BAC和△DAE中
∵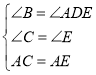 ..
..
∴△ABC≌△ADE(AAS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.
(1)求△ABC的面积;
(2)求CD的长;
(3)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(4)作出△BCD的边BC上的高DF,当BD=
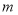 时,试求出DF的长(用
时,试求出DF的长(用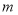 表示).
表示).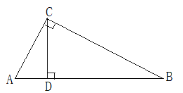
-
科目: 来源: 题型:
查看答案和解析>>【题目】口袋中装有四个大小完全相同的小球,把它们分别标号1,2,3,4,从中随机摸出一个球,记下数字后放回,再从中随机摸出一个球,利用树状图或者表格求出两次摸到的小球数和等于4的概率.
【答案】
 .
.【解析】试题分析:
根据题意列表如下,由表可以得到所有的等可能结果,再求出所有结果中,两次所摸到小球的数字之和为4的次数,即可计算得到所求概率.
试题解析:
列表如下:
1
2
3
4
1
(1,1)
(1,2)
(1,3)
(1,4)
2
(2,1)
(2,2)
(2,3)
(2,4)
3
(3,1)
(3,2)
(3,3)
(3,4)
4
(4,1)
(4,2)
(4,3)
(4,4)
由表可知,共有16种等可能事件,其中两次摸到的小球数字之和等于4的有(3,1)、(2,2)和(1,3),共计3种,
∴P(两次摸到小球的数字之和等于4)=
 .
.【题型】解答题
【结束】
23【题目】小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区组织“献爱心手拉手”捐款活动.对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图和统计表(图中信息不完整).已知A、B两组捐款户数的比为1:5.请结合以上信息解答下列问题.捐款户数分组统计表
(1)本次调查了 户;
(2)补全“捐款户数分组统计表”和“捐款户数分组统计图1”;
(3)若该社区有2000户住户,请根据以上信息,估计全社区捐款不少于150元的户数.


-
科目: 来源: 题型:
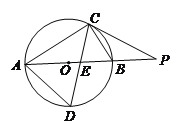
查看答案和解析>>【题目】如图,⊙O的直径AB为2cm,弦BC为1cm,∠ACB的平分线与⊙O交于点D,与AB交于点E,P为AB延长线上一点,连接PC,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
-
科目: 来源: 题型:
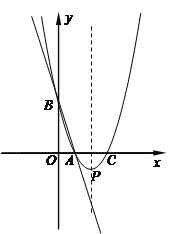
查看答案和解析>>【题目】如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.
(1)求a,k的值;
(2)抛物线的对称轴上是否存在一点M,使△ABM的周长最小,若存在,求出△ABM的周长;若不存在,请说明理由;
(3)若以AB为直径画圆,与抛物线的对称轴交于点N,求出点N坐标.
-
科目: 来源: 题型:
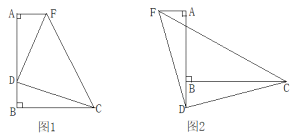
查看答案和解析>>【题目】已知∠ABC=90°,D是直线AB边上的点,AD=BC
(1)如图1,点D在线段AB上,过点A作AF⊥AB,且AF=BD,连接DC、DF、CF,试判断△CDF的形状并说明理由;
(2)如图2,点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,以上结论是否仍然成立?请说明理由.
相关试题

