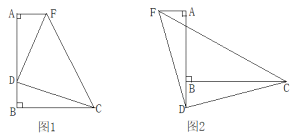
【题目】已知∠ABC=90°,D是直线AB边上的点,AD=BC
(1)如图1,点D在线段AB上,过点A作AF⊥AB,且AF=BD,连接DC、DF、CF,试判断△CDF的形状并说明理由;
(2)如图2,点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,以上结论是否仍然成立?请说明理由.
参考答案:
【答案】(1)△CDF是等腰直角三角形,理由见解析;(2)成立,理由见解析.
【解析】
(1)根据题意先证明出△FAD和△DBC全等,然后得出DF=DC,进一步利用全等三角形性质以及等量代换求出∠FDC=90°,从而证明出△CDF是等腰直角三角形;
(2)根据题意先证明出△FAD和△DBC全等,然后得出DF=DC,进一步利用全等三角形性质以及等量代换求出∠FDC=90°,从而证明出△CDF是等腰直角三角形;
(1)△CDF是等腰直角三角形,理由如下:
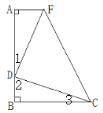
∵AF⊥AB,
∴∠A=90°
在△FAD和△DBC中
∵ ..
..
∴△FAD≌△DBC(SAS),
∴∠1=∠3,DF=DC,
∵∠2+∠3=90°,
∴∠1+∠2=90°,
∴∠FDC=180°90°=90°,
又∵DF=DC,
∴△CDF是等腰直角三角形;
(2)仍然成立,理由如下:
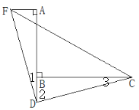
∵AF⊥AB,
∴∠A=90°.
在△FAD和△DBC中
∵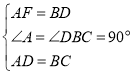 .
.
∴△FAD≌△DBC(SAS),
∴∠1=∠3,DF=DC,
∵∠2+∠3=90°,
∴∠1+∠2=90°,即∠FDC=90°,
又∵DF=DC,
∴△CDF是等腰直角三角形.
-
科目: 来源: 题型:
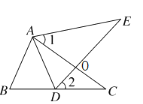
查看答案和解析>>【题目】如图,在△ABC中,点D在线段BC上,∠1=∠2,AE=AC.
(1)在不添加任何字母的情况下,请再补充一个条件,使得△ABC≌△ADE,你补充的条件是 (至少写出两个可行的条件);
(2)请你从所给条件中选一个,使△ABC≌△ADE,并证明.
-
科目: 来源: 题型:
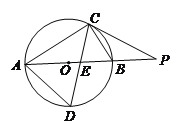
查看答案和解析>>【题目】如图,⊙O的直径AB为2cm,弦BC为1cm,∠ACB的平分线与⊙O交于点D,与AB交于点E,P为AB延长线上一点,连接PC,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
-
科目: 来源: 题型:
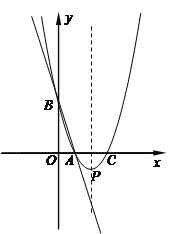
查看答案和解析>>【题目】如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.
(1)求a,k的值;
(2)抛物线的对称轴上是否存在一点M,使△ABM的周长最小,若存在,求出△ABM的周长;若不存在,请说明理由;
(3)若以AB为直径画圆,与抛物线的对称轴交于点N,求出点N坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
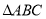 中,
中,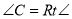 ,
, ,
, .若动点
.若动点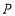 从点
从点 开始,沿
开始,沿 的路径运动,且速度为每秒
的路径运动,且速度为每秒 ,设运动的时间为
,设运动的时间为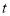 秒,当
秒,当 ______时,
______时, 为等腰三角形.
为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级准备购买一批笔记本奖励优秀学生,在购买时发现,每本笔记本可以打九折,用360元钱购买的笔记本,打折后购买的数量比打折前多10本.
(1)求打折前每本笔记本的售价是多少元?
(2)由于考虑学生的需求不同,学校决定购买笔记本和笔袋共90件,笔袋每个原售价为6元,两种物品都打九折,若购买总金额不低于360元,且不超过365元,问有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB、AC上,AD交EF于点H.
(1)当矩形EFPQ为正方形时,求正方形的边长;
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求出最大面积;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线BC匀速向右运动(当矩形的顶点Q到达C点时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.

相关试题

