【题目】已知一次函数![]() .回答下列问题:
.回答下列问题:
(1)求出它的图像与坐标轴的交点坐标;
(2)当自变量![]() 满足什么条件时?函数值
满足什么条件时?函数值![]() ?
?
(3)当自变量![]() 时,则函数值
时,则函数值![]() 的范围?
的范围?
(4)在所给的直角坐标系中,画出直线![]() 的图像.
的图像.
参考答案:
【答案】(1)![]() ,
,![]() . (2)当
. (2)当![]() 时,
时,![]() . (3)当
. (3)当![]() 时,
时,![]() . (4)见解析.
. (4)见解析.
【解析】
(1)分别将![]() 和
和![]() 代入
代入![]() 中,即可求出交点坐标;
中,即可求出交点坐标;
(2)根据![]() ,可得y随x的增大而减小,当
,可得y随x的增大而减小,当![]() 时
时![]() ,故可得当
,故可得当![]() 时,
时,![]() ;
;
(3)根据![]() ,可得y随x的增大而减小,当
,可得y随x的增大而减小,当![]() 时
时![]() ,当
,当![]() 时
时![]()
故可得当![]() 时,
时,![]() ;
;
(4)作出(1)中的交点坐标,作过交点的直线即可.
(1)将![]() 代入
代入![]() 中
中
![]()
将![]() 代入
代入中
![]()
解得![]()
故它的图象与坐标轴的交点坐标为![]() 和
和![]() .
.
(2)∵![]()
∴y随x的增大而减小
∵当![]() 时
时![]()
∴当![]() 时,
时,![]() .
.
(3)∵![]()
∴y随x的增大而减小
∵当![]() 时
时![]() ,当
,当![]() 时
时![]()
∴当![]() 时,
时,![]() .
.
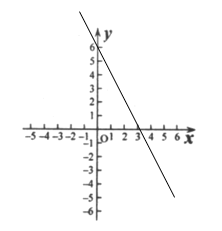
(4)如图所示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=
 ,OC=
,OC=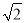 ,则另一直角边BC的长为__________.
,则另一直角边BC的长为__________.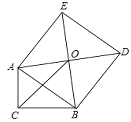
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球
两红
一红一白
两白
礼金券(元)
18
24
18
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接BM,DN.
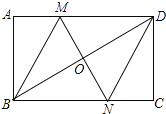
(1)求证:四边形BMDN是菱形;
(2)若AB=2,AD=4,求MD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两条公路
 、
、 交予点
交予点 ,在公路
,在公路 旁有一学校
旁有一学校 ,与
,与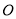 点的距离为
点的距离为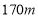 ,点
,点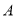 (学校)到公路
(学校)到公路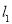 的距离
的距离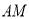 为
为 .一大货车从
.一大货车从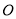 点出发,行驶在公路
点出发,行驶在公路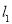 上,汽车周围
上,汽车周围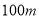 范围内有噪音影响.
范围内有噪音影响.(1)货车开过学校是否受噪音影响?为什么?
(2)若汽车速度为
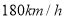 ,则学校受噪音影响多少秒钟?
,则学校受噪音影响多少秒钟?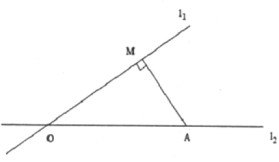
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的四个顶点分别在反比例函数y=
 与y=
与y= (x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与x轴交于点
与x轴交于点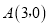 ,与y轴交于点B,抛物线
,与y轴交于点B,抛物线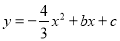 经过点
经过点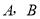 .
.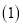 求k的值和抛物线的解析式;
求k的值和抛物线的解析式;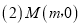 为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点
为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点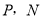 .
. 若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.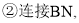 当
当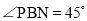 时,求m的值.
时,求m的值. 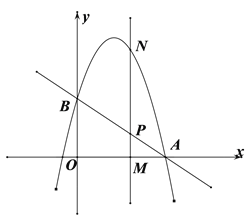
相关试题

