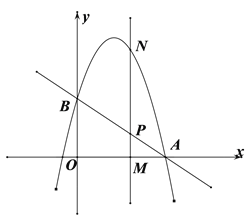
【题目】如图,直线![]() 与x轴交于点
与x轴交于点![]() ,与y轴交于点B,抛物线
,与y轴交于点B,抛物线![]() 经过点
经过点![]() .
.
![]() 求k的值和抛物线的解析式;
求k的值和抛物线的解析式;
![]() 为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点
为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点![]() .
.
![]() 若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
![]() 当
当![]() 时,求m的值.
时,求m的值.
参考答案:
【答案】⑴![]() ,
, ![]() ⑵
⑵![]() ⑶有两解,N点在AB的上方或下方, m=
⑶有两解,N点在AB的上方或下方, m=![]() 与m=
与m=![]()
【解析】整体分析:
(1)把A(3,0)代入y=kx+2中求k值,把x=0代入y=kx+2,求出B点的坐标,由A,B的坐标求二次函数的解析式;(2)①用含m的式子表示出NP的长,由平行四边形的性质得OB=PN列方程求解;②连接BN,过点B作BN的垂线交x轴于点G,过点G作BA的垂线,垂足为点H, 设GH=BH=t,由![]() ,用t表示AH,AG,由AB=
,用t表示AH,AG,由AB=![]() ,求t的值,求直线BG,BN的解析式,分别与抛物线方程联立求解.
,求t的值,求直线BG,BN的解析式,分别与抛物线方程联立求解.
解:⑴![]() ,
,
二次函数的表达式为![]()
⑵如图,设M(m,0),
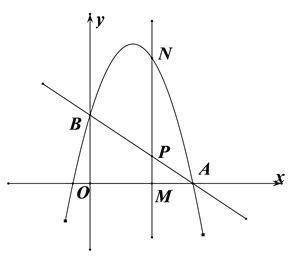
则p(m, ![]() ),N(m,
),N(m, ![]()
![]() =
=![]()
=![]()
由于四边形OBNP为平行四边形得PN=OB=2,
解方程![]() .
.
即![]()
⑶有两解,N点在AB的上方或下方,m=![]() 与m=
与m=![]() .
.
如图连接BN,过点B作BN的垂线交x轴于点G,过点G作BA的垂线,垂足为点H.
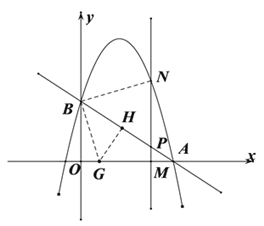
由![]() 得
得![]() ,
,
从而设GH=BH=t,则由![]() ,得AH=
,得AH= ![]() ,
,
由AB=t+ ![]() =
=![]() ,解得t=
,解得t=![]() ,
,
从而OG=OA-AG=3-![]() =
=![]() .即G(
.即G(![]() )
)
由B(0,2),G(![]() )得
)得![]() .
.
将![]() 分别与
分别与![]() 联立,
联立,
解方程组得m=![]() ,m=
,m=![]() .
.
故m=![]() 与m=
与m=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
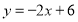 .回答下列问题:
.回答下列问题:(1)求出它的图像与坐标轴的交点坐标;
(2)当自变量
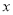 满足什么条件时?函数值
满足什么条件时?函数值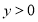 ?
?(3)当自变量
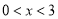 时,则函数值
时,则函数值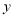 的范围?
的范围?(4)在所给的直角坐标系中,画出直线
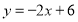 的图像.
的图像.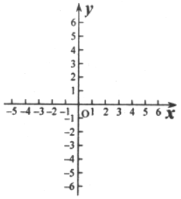
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两条公路
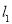 、
、 交予点
交予点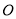 ,在公路
,在公路 旁有一学校
旁有一学校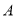 ,与
,与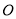 点的距离为
点的距离为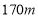 ,点
,点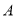 (学校)到公路
(学校)到公路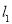 的距离
的距离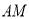 为
为 .一大货车从
.一大货车从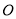 点出发,行驶在公路
点出发,行驶在公路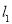 上,汽车周围
上,汽车周围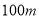 范围内有噪音影响.
范围内有噪音影响.(1)货车开过学校是否受噪音影响?为什么?
(2)若汽车速度为
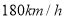 ,则学校受噪音影响多少秒钟?
,则学校受噪音影响多少秒钟?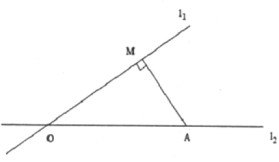
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的四个顶点分别在反比例函数y=
 与y=
与y= (x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于( )

A. 75° B. 60° C. 45° D. 30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=70°,⊙O切CA、CB分别于点A和点B,则弦AB所对的圆周角的度数为( )
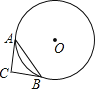
A. 110° B. 55° C. 55°或 110° D. 55 或 125°
相关试题

