【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接BM,DN.
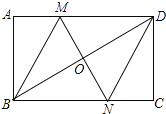
(1)求证:四边形BMDN是菱形;
(2)若AB=2,AD=4,求MD的长.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】
试题分析:(1)根据矩形性质求出AD∥BC,推出∠MDO=∠NBO,∠DMO=∠BNO,证△DMO≌△BNO,推出OM=ON,得出平行四边形BMDN,推出菱形BMDN;
(2)根据菱形性质求出DM=BM,在Rt△AMB中,根据勾股定理得出BM2=AM2+AB2,即可列方程求得.
(1)证明:∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
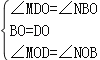
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形.
(2)解:∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(4﹣x)2+22,
解得:x=![]() ,
,
答:MD长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a2﹣a2=1 B.(a+b)2=a2+b2
C.(3b3)2=6b6 D.(﹣a)5÷(﹣a)3=a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(x+1)(x2﹣x+1)的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2-4x+1=0时,配方后所得的方程是( )
A. (x-2)2=1 B. (x-2)2=-1 C. (x-2)2=3 D. (x+2)2=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次汉字听写大赛中,10名学生得分情况如表:
人数
3
4
2
1
分数
80
85
90
9595
那么这10名学生所得分数的中位数和众数分别是( )
A.85和82.5 B.85.5和85 C.85和85 D.85.5和80
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,有下列结论:
①a<0,②b<0,③c>0,④4a﹣2b+c<0,⑤b+2a=0
其中正确的个数有( )
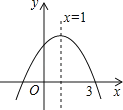
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】宁波地铁1号线二期于2016年3月19日开通试运营,当天客流量超25万人次,数据25万用科学记数法表示为( )
A.2.5×104 B.2.5×105 C.0.25×105 D.0.25×106
相关试题

