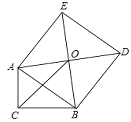
【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=![]() ,OC=
,OC=![]() ,则另一直角边BC的长为__________.
,则另一直角边BC的长为__________.
参考答案:
【答案】![]()
【解析】分析:如图所示,过O作OF⊥BC,过A作AM⊥OF,证明△AOM≌△BOF,根据全等三角形的可得AM=OF,OM=FB,再证明四边形ACFM为矩形,根据矩形的性质可得AM=CF,AC=MF=![]() ,在等腰直角三角形△OCF中,根据勾股定理求得CF=OF=1,再求得FM=
,在等腰直角三角形△OCF中,根据勾股定理求得CF=OF=1,再求得FM=![]() ,根据BC=CF+BF即可求得BC的长.
,根据BC=CF+BF即可求得BC的长.
详解:如图所示,过O作OF⊥BC,过A作AM⊥OF,

∵四边形ABDE为正方形,
∴∠AOB=90°,OA=OB,
∴∠AOM+∠BOF=90°,
又∠AMO=90°,
∴∠AOM+∠OAM=90°,
∴∠BOF=∠OAM,
在△AOM和△BOF中, 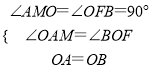 ,
,
∴△AOM≌△BOF(AAS),
∴AM=OF,OM=FB,
又∠ACB=∠AMF=∠CFM=90°,
∴四边形ACFM为矩形,
∴AM=CF,AC=MF=![]() ,
,
∴OF=CF,
∴△OCF为等腰直角三角形,
∵OC=![]() ,
,
∴根据勾股定理得:CF2+OF2=OC2,
解得:CF=OF=1,
∴FB=OM=OF-FM=1-![]() =
=![]() ,
,
则BC=CF+BF=![]() .
.
故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则
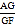 的值是( )
的值是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】天山旅行社为吸引游客组团去具有喀斯特地貌特征的黄果树风景区旅游,推出了如下收费标准(如图所示):

某单位组织员工去具有喀斯特地貌特征的黄果树风景区旅游,共支付给旅行社旅游费用27000元,请问该单位这次共有多少名员工去具有喀斯特地貌特征的黄果树风景区旅游?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A.B在反比例函数y=
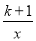 的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( )
的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( )
A.5B.-5C.4D.-4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球
两红
一红一白
两白
礼金券(元)
18
24
18
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接BM,DN.
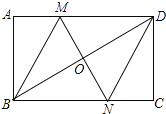
(1)求证:四边形BMDN是菱形;
(2)若AB=2,AD=4,求MD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
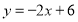 .回答下列问题:
.回答下列问题:(1)求出它的图像与坐标轴的交点坐标;
(2)当自变量
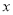 满足什么条件时?函数值
满足什么条件时?函数值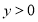 ?
?(3)当自变量
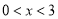 时,则函数值
时,则函数值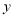 的范围?
的范围?(4)在所给的直角坐标系中,画出直线
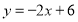 的图像.
的图像.
相关试题

