【题目】如图,在由边长为1的小正方形组成的网格中,三角形ABC的顶点均落在格点上.
(1)将△ABC绕点O顺时针旋转90°后,得到△A1B1C1 . 在网格中画出△A1B1C1;
(2)求线段OA在旋转过程中扫过的图形面积;(结果保留π)
(3)求∠BCC1的正切值.
参考答案:
【答案】
(1)
解:如图.
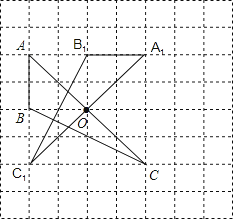
△A1B1C1即为所求三角形
(2)
解:由勾股定理可知OA= ![]() =2
=2 ![]() ,
,
线段OA在旋转过程中扫过的图形为以OA为半径,∠AOA1为圆心角的扇形,
则S扇形OAA1= ![]() =2π.
=2π.
答:扫过的图形面积为2π
(3)
解:在Rt△BCC1中,tan∠BCC1= ![]() =
= ![]() =
= ![]() .
.
答:∠BCC1的正切值是 ![]()
【解析】(1)根据图形旋转的性质画出旋转后的图形即可;(2)先根据勾股定理求出OA的长,再根据线段OA在旋转过程中扫过的图形为以OA为半径,∠AOA1为圆心角的扇形,利用扇形的面积公式得出结论即可;(3)直接根据锐角三角函数的定义即可得出结论.
【考点精析】利用扇形面积计算公式和锐角三角函数的定义对题目进行判断即可得到答案,需要熟知在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2);锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形纸片ABCD中,
 ,
, ,将纸片折叠,使C,D落在AB边上的
,将纸片折叠,使C,D落在AB边上的 ,
, 处,折痕为MN,则
处,折痕为MN,则 ______度.
______度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)计算: 9 + ( π 2010 ) 0 2 cos 45 ° .
(2)先化简,再求值: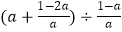 ,其中a=1﹣
,其中a=1﹣ 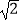 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形……,如此操作下去,那么,第6个三角形的直角顶点坐标为( )

A. (﹣
 ,
, ) B. (﹣
) B. (﹣ ,
, ) C. (﹣
) C. (﹣ ,
, ) D. (﹣
) D. (﹣ ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,
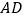 平分
平分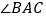 ,
,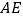 ⊥
⊥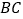 ,
,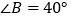 ,
,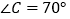 .
.【1】求
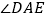 的度数
的度数【2】如图②,若把“
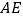 ⊥
⊥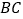 ”变成“点F在DA的延长线上,
”变成“点F在DA的延长线上,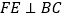 ”,其它条件不变,求
”,其它条件不变,求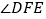 的度数;
的度数;【3】如图③,若把“
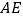 ⊥
⊥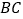 ”变成“
”变成“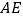 平分
平分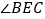 ”,其它条件不变,
”,其它条件不变,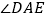 的大小是否变化,并请说明理由.(此题9分)
的大小是否变化,并请说明理由.(此题9分)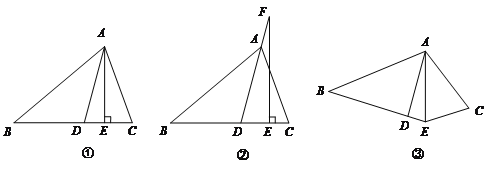
-
科目: 来源: 题型:
查看答案和解析>>【题目】自开展“学生每天锻炼1小时”活动后,我市某中学根据学校实际情况,决定开设A:毽子,B:篮球,C:跑步,D:跳绳四种运动项目.为了了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图统计图.请结合图中信息解答下列问题:

(1)该校本次调查中,共调查了多少名学生?
(2)请将两个统计图补充完整;
(3)在本次调查的学生中随机抽取1人,他喜欢“跑步”的概率有多大? -
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车销售公司经销某品牌A、B两款汽车,已知A款汽车每辆进价为
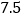 万元,B款汽车每辆进价为6万元.
万元,B款汽车每辆进价为6万元. 公司预计用不多于135万元且不少于129万元的资金购进这两款汽车共20辆,有几种进货方案,它们分别是什么?
公司预计用不多于135万元且不少于129万元的资金购进这两款汽车共20辆,有几种进货方案,它们分别是什么? 如果A款汽车每辆售价为9万元,B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使
如果A款汽车每辆售价为9万元,B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使 中所有的方案获利相同,a值应是多少,此种方案是什么?(提示:可设购进B款汽车x辆)
中所有的方案获利相同,a值应是多少,此种方案是什么?(提示:可设购进B款汽车x辆)
相关试题

