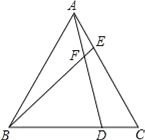
【题目】如图,已知△ABC为等边三角形(三条边相等三个角为60°的三角形),点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)求∠BFD的度数.
参考答案:
【答案】(1)见解析;(2)60°.
【解析】试题分析:(1)根据等边三角形的性质根据SAS即可证明△ABE≌△CAD;
(2)由三角形全等可以得出∠ABE=∠CAD,由外角与内角的关系就可以得出结论.
试题解析:(1)∵△ABC为等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=∠BAC=60°.
在△ABE和△CAD中,
AB=CA, ∠BAC=∠C,AE =CD,
∴△ABE≌△CAD(SAS),
(2)∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∵∠BAD+∠CAD=60°,
∴∠BAD+∠EBA=60°,
∵∠BFD=∠ABE+∠BAD,
∴∠BFD=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.
(1)若CF交⊙O于点G,⊙O的半径是4,求
 的长;
的长;(2)请判断直线BF与⊙O的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).

(1)观察每次变换前后的三角形有何变化,找出规律,按些变换规律将△OA3B3变换成△OA4B4,则A4的坐标是_______,B4的坐标是_________.
(2)若按第(1)题的规律将△OAB进行了n次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,请推测An的坐标是_______,Bn的坐标是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.
●特例感知
①等腰直角三角形 勾股高三角形(请填写“是”或者“不是”);
②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若
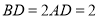 ,试求线段CD的长度.
,试求线段CD的长度.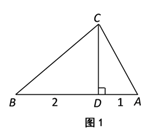
●深入探究
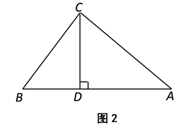
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;
●推广应用
如图3,等腰△ABC为勾股高三角形,其中
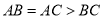 ,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若
,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若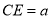 ,试求线段DE的长度.
,试求线段DE的长度.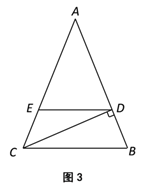
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形的长是2x+3y,宽是x+y,则这个长方形的周长是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】买一个篮球需要m元,买一个排球需要n元,则买1个篮球和2个排球共需_______元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
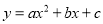 与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣
与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣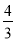 ≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程
≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程 有两个不相等的实数根,其中正确的有( )
有两个不相等的实数根,其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
相关试题

