【题目】在△ABC中,∠ACB=90°,D是AB的中点,过点B作∠CBE=∠A,BE与射线CA相交于点E,与射线CD相交于点F.
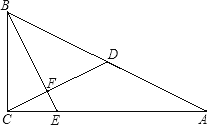
(1)如图,当点E在线段CA上时,求证:BE⊥CD;
(2)若BE=CD,那么线段AC与BC之间具有怎样的数量关系?并证明你所得到的结论;
(3)若△BDF是等腰三角形,求∠A的度数.
参考答案:
【答案】(1)证明见解析;(2)AC=2BC;(3)22.5°或67.5°.
【解析】
(1)根据角之间的等量关系及中点的特点即可得出答案;
(2)根据题意易证△BCE∽△ACB,根据相似三角形比例关系即可得出结论;
(3)分①点E在线段CA上时;②点E在线段CA延长线上讨论求解.
(1)∵∠ACB=90°,D是AB的中点,∴CD=AD,∴∠A=∠DCA.
∵∠CBE=∠A,∴∠DCA=∠CBE.
∵∠CBE+∠BEC=90°,∴∠BEC+∠DCA =90°,∴BE⊥CD;
(2)线段AC与BC之间的数量关系是:AC=2BC.
∵∠CBE=∠A,∠BCE=∠ACB,∴△BCE∽△ACB,∴![]() .
.
∵BE=CD,![]() ,∴
,∴![]() ,∴AC=2BC.
,∴AC=2BC.
(3)∵△BDF是等腰三角形,∠BFD=90°,∴∠BDF=45°.
①当点E在线段CA上时,如图1,∠A![]() ∠BDF=22.5°;
∠BDF=22.5°;
②当点E在线段CA延长线上时,如图2,∠CDA=∠BDF=45°,∠BAC![]() .
.
综上所述:∠BAC的度数为22.5°或67.5°.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.

(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号内:
-35,0.1,
 ,0,
,0,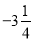 ,1,4.01001000···,22,-0.3,
,1,4.01001000···,22,-0.3, ,
, .
.正数:{ ,···};
整数:{ ,···};
负分数:{ ,···};
非负整数:{ ,···}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某九年一贯制学校在六年级和九年级的男生中分别随机抽取40名学生测量他们的身高,将数据分组整理后,绘制的频数分布直方图如下:其中两条纵向虚线上端的数值分别是每个年级抽出的40名男生身高的平均数,根据统计图提供的信息,下列结论不合理的是( )

A. 六年级40名男生身高的中位数在第153~158cm组
B. 可以估计该校九年级男生的平均身高比六年级的平均身高高出18.6cm
C. 九年级40名男生身高的中位数在第168~173cm组
D. 可以估计该校九年级身高不低于158cm但低于163cm的男生所占的比例大约是5%
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵ ,(已知)
∴∠AGD= (等式性质)

-
科目: 来源: 题型:
查看答案和解析>>【题目】南江县某乡
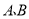 两村盛产凤柑,
两村盛产凤柑,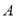 村有凤柑200吨,
村有凤柑200吨,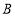 村有凤柑300吨.现将这些凤柑运到
村有凤柑300吨.现将这些凤柑运到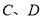 两个冷藏仓库,已知
两个冷藏仓库,已知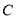 仓库可储存240吨,
仓库可储存240吨,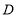 仓库可储存260吨;从
仓库可储存260吨;从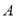 村运往
村运往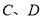 两处的费用分别为每吨20元和25元,从
两处的费用分别为每吨20元和25元,从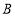 村运往
村运往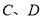 两处的费用分别为每吨15元和18元.设从
两处的费用分别为每吨15元和18元.设从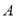 村运往
村运往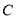 仓库的凤柑重量为
仓库的凤柑重量为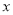 吨.
吨.(1)请填写表格(单位:吨)
(2)请分别求出
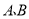 两村运往两仓库的凤柑的运输费用(用含
两村运往两仓库的凤柑的运输费用(用含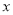 的代数式表示);
的代数式表示);(3)当
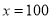 时,试求
时,试求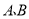 两村运往两仓库的凤柑的运输费用.
两村运往两仓库的凤柑的运输费用.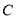
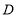
总计
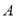
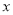
200
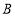
300
总计
240
260
500
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示,下列叙述正确的是( )

A. 甲乙两地相距1200千米
B. 快车的速度是80千米∕小时
C. 慢车的速度是60千米∕小时
D. 快车到达甲地时,慢车距离乙地100千米
相关试题

