搜索
【题目】单项式﹣5ab2的系数是 ， 次数是 ．
参考答案：
【答案】-5；3
【解析】解：根据单项式系数、次数的定义可知：单项式﹣5ab2的系数是﹣5，次数是3．
【考点精析】根据题目的已知条件，利用单项式的相关知识可以得到问题的答案，需要掌握在代数式中，若只含有乘法（包括乘方）运算．或虽含有除法运算，但除式中不含字母的一类代数式叫单项式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】游泳是一项深受青少年喜爱的体育活动，学校为了加强学生的安全意识，组织学生观看了纪实片“孩子，请不要私自下水”，并于观看后在本校的2000名学生中作了抽样调查、请根据下面两个不完整的统计图回答以下问题
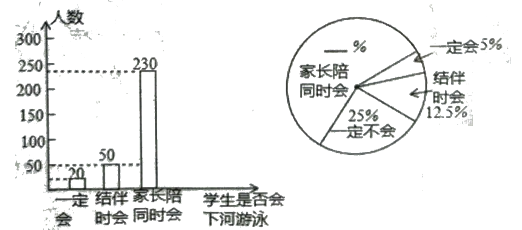
(1)这次抽样调查中，共调查了 名学生
(2)“家长陪同时会”的学生所占比例为 %，"一定不会"的学生有 人
(3)根据抽样调查的结果，估算该校2000名学生中大约有多少人“一定会下河游泳”?
-
科目： 来源： 题型：
查看答案和解析>>【题目】某一线城市对出租车营运价进行了调整，调价前后的收费标准对比如下:调整前,3公里及3公里以内12.5元，3公里后里程价2.4元/公里，无返空费；调整后, 2公里及2公里以内10元，2公里后里程价2.4元/公里，超过25公里部分，按里程价的30%加收返空费．
（1）请你帮忙计算一下，调价后，若乘客乘坐出租车的行程为8公里，他比以前少付了多少钱（不考虑红灯等因素）？
（2）网上流传“24公里换车”规避返空费，即乘客的行程超过25公里，就在24公里处下车，换乘另一辆出租车．但其实并不是所有行程超过25公里的乘客都需要换车．
例如：①若行程为30公里：不换车，总费用为：
10+23×2.4+5×2.4×130%=80.8元；
换车，总费用为：10+22×2.4+10+4×2.4＝82.4元，因此，行程30公里若换车，则费用反而增加2.4元．
②若行程为40公里，不换车，总费用为：
10+23×2.4+15×2.4×130%=112元，若换车，总费用为：10+22×2.4+10+2.4×14＝106.4元，则可节约5.6元．
若设行程为x 公里（26＜x＜48 ），请用含x的式子分别表示出不换车的费用和换车的费用，并帮忙计算一下，行程超过多少公里后换车会就会节约费用（不考虑红灯等因素）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料： 解答“已知x﹣y=2，且x＞1，y＜0，试确定x+y的取值范围”有如下解法：
解：∵x﹣y=2，又∵x＞1，∴y+2＞1，即y＞﹣1
又y＜0，∴﹣1＜y＜0．…①
同理得：1＜x＜2．…②
由①+②得﹣1+1＜y+x＜0+2，∴x+y的取值范围是0＜x+y＜2．
请按照上述方法，完成下列问题：
已知关于x、y的方程组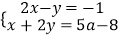
的解都为非负数．
（1）求a的取值范围；
（2）已知2a﹣b=1，且，求a+b的取值范围；
（3）已知a﹣b=m（m是大于1的常数），且b≤1，求2a+b最大值．（用含m的代数式表示） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线y=-2x经过点P(-2,a)，点P关于y轴的对称点P'在反比例函数y =
(k≠0)的图像上。(1)求a的值
(2)直接写出点P'的坐标
(3)求反比例函数的解析式
-
科目： 来源： 题型：
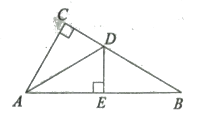
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，AD平分∠CAB,交CB于点D,DE⊥AB于点E.
(1)求证：△ACD≌△AED
(2)若AC=5，△DEB的周长为8，求△ABC的周长
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y＝2(x－1)2的对称轴是（ ）
A. 1 B. 直线x＝1
C. 直线x＝2 D. 直线x＝－1
相关试题
