【题目】游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的2000名学生中作了抽样调查、请根据下面两个不完整的统计图回答以下问题
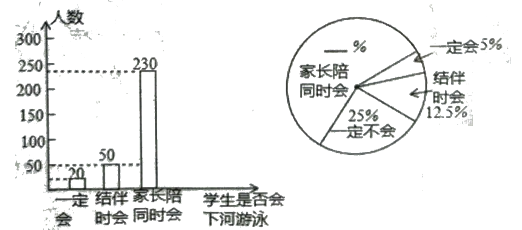
(1)这次抽样调查中,共调查了 名学生
(2)“家长陪同时会”的学生所占比例为 %,"一定不会"的学生有 人
(3)根据抽样调查的结果,估算该校2000名学生中大约有多少人“一定会下河游泳”?
参考答案:
【答案】(1)400人;(2)57.5;100人;(3)100人.
【解析】试题分析:(1)根据一定会的人数和所占的百分比即可求出总人数;
(2)用总人数减去其它人数得出不会的人数,再根据家长陪同的人数除以总人数得出家长陪同时会的所占的百分比;
(3)用2000乘以一定会下河游泳所占的百分百,即可求出该校一定会下河游泳的人数.
试题解析:(1)总人数是:20÷5%=400(人);
(2)家长陪同的所占的百分百是![]() ×100%=57.5%,
×100%=57.5%,
一定不会的人数是400﹣20﹣50﹣230=100(人),
(3)根据题意得:2000×5%=100(人).
答:该校2000名学生中 “一定会下河游泳”大约有100人.
-
科目: 来源: 题型:
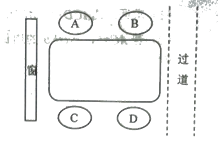
查看答案和解析>>【题目】莫菲、隆迪、紫惠和曲代4人一起去火锅店吃火锅,4人在如图所示的四人桌前就座,其中莫菲和紫惠坐在餐桌的同侧,
(1)请用适当的方法表示出所有的不同就座方案.
(2)请问隆迪恰好坐在靠近过道一侧的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】实践操作如图,∠△ABC是直角三角形,∠ACB=90,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作∠BAC的平分线,交BC于点0
②以点0为圆心,OC为半径作圆.综合运用在你所作的图中,
(1)直线AB与⊙0的位置关系是
(2)证明:BA·BD=BC·BO;
(3)若AC=5,BC=12,求⊙0的半径

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=3(x﹣1)2+5的最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一线城市对出租车营运价进行了调整,调价前后的收费标准对比如下:调整前,3公里及3公里以内12.5元,3公里后里程价2.4元/公里,无返空费;调整后, 2公里及2公里以内10元,2公里后里程价2.4元/公里,超过25公里部分,按里程价的30%加收返空费.
(1)请你帮忙计算一下,调价后,若乘客乘坐出租车的行程为8公里,他比以前少付了多少钱(不考虑红灯等因素)?
(2)网上流传“24公里换车”规避返空费,即乘客的行程超过25公里,就在24公里处下车,换乘另一辆出租车.但其实并不是所有行程超过25公里的乘客都需要换车.
例如:①若行程为30公里:不换车,总费用为:
10+23×2.4+5×2.4×130%=80.8元;
换车,总费用为:10+22×2.4+10+4×2.4=82.4元,因此,行程30公里若换车,则费用反而增加2.4元.
②若行程为40公里,不换车,总费用为:
10+23×2.4+15×2.4×130%=112元,若换车,总费用为:10+22×2.4+10+2.4×14=106.4元,则可节约5.6元.
若设行程为x 公里(26<x<48 ),请用含x的式子分别表示出不换车的费用和换车的费用,并帮忙计算一下,行程超过多少公里后换车会就会节约费用(不考虑红灯等因素).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料: 解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,又∵x>1,∴y+2>1,即y>﹣1
又y<0,∴﹣1<y<0.…①
同理得:1<x<2.…②
由①+②得﹣1+1<y+x<0+2,∴x+y的取值范围是0<x+y<2.
请按照上述方法,完成下列问题:
已知关于x、y的方程组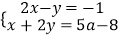 的解都为非负数.
的解都为非负数.
(1)求a的取值范围;
(2)已知2a﹣b=1,且,求a+b的取值范围;
(3)已知a﹣b=m(m是大于1的常数),且b≤1,求2a+b最大值.(用含m的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣5ab2的系数是 , 次数是 .
相关试题

