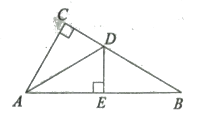
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE⊥AB于点E.
(1)求证:△ACD≌△AED
(2)若AC=5,△DEB的周长为8,求△ABC的周长
参考答案:
【答案】(1)证明见解析;
(2)△ABC的周长是18.
【解析】试题分析:(1)、根据角平分线的性质得出DC=DE,结合AD=AD从而得出两个直角三角形全等;(2)、根据全等得出AE=AC=5,CD=ED,从而得出△ABC的周长=AC+AC+△DEB的周长得出答案.
试题解析:(1)、因为AD平分∠CAB,∠C=90°,DE⊥AB 所以DC=DE
在△ACD和△AED中,DC=DE,AD=AD 得△ACD≌△AED(HL)
(2)由(1)得△ACD≌△AED 所以AE=AC=5,CD=ED
![]() =AC+AB+BC=AC+(AE+EB)+(BD+DC)=AC+AC+EB+BD+DE)=AC+AC+
=AC+AB+BC=AC+(AE+EB)+(BD+DC)=AC+AC+EB+BD+DE)=AC+AC+![]() =5+5+8=18.
=5+5+8=18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料: 解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,又∵x>1,∴y+2>1,即y>﹣1
又y<0,∴﹣1<y<0.…①
同理得:1<x<2.…②
由①+②得﹣1+1<y+x<0+2,∴x+y的取值范围是0<x+y<2.
请按照上述方法,完成下列问题:
已知关于x、y的方程组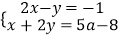 的解都为非负数.
的解都为非负数.
(1)求a的取值范围;
(2)已知2a﹣b=1,且,求a+b的取值范围;
(3)已知a﹣b=m(m是大于1的常数),且b≤1,求2a+b最大值.(用含m的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣5ab2的系数是 , 次数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=-2x经过点P(-2,a),点P关于y轴的对称点P'在反比例函数y =
 (k≠0)的图像上。
(k≠0)的图像上。(1)求a的值
(2)直接写出点P'的坐标
(3)求反比例函数的解析式

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2(x-1)2的对称轴是( )
A. 1 B. 直线x=1
C. 直线x=2 D. 直线x=-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,△ABC中,D是BC边上一点,则△BD与△ADC有一个相同的高,它们的面积之比等于相应的底之比,记为
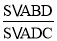 =
=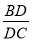 (△ABD、△ADC的面积分别用S△ABD、S△ADC表示)。现有BD=
(△ABD、△ADC的面积分别用S△ABD、S△ADC表示)。现有BD=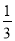 BC,则S△ABD:S△ADC=
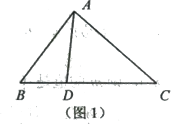
BC,则S△ABD:S△ADC= (2)如图2,△ABC中,E、F分别是BC、AC边上一点,且有BE:EC=1:2,AF: FC=1:1,AE与BF相交于点G、现作EH ∥BF交AC于点H、依次求FH :HC、AG: GE、BG:GF的值
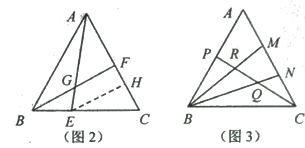
(3)如图3,△ABC中,点P在边AB上,点M、N在边AC上,且有AP=PB,AM=MN=NC,BM、BW与CP分别相交于点R、Q.,现已知△ABC的面积为1,求△BRQ的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售某一种新型通讯产品,已知每件产品的进价为4万元,每月销售该种产品的总开支(不含进价)总计11万元.在销售过程中发现,月销售量夕(件)与销售单价x (万元)之间存在着如图所示的一次函数关系、
(1)求y关于x的函数关系式(直接写出结果)
(2)试写出该公司销售该种产品的月获利z(万元)关于销售单价x(万元)的函数关系式、当销售单价x为何值时,月获利最大?并求这个最大值(月获利一月销售额一月销售产品总进价一月总开支)
(3)若公司希望该产品一个月的销售获利不低于5万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少万元

相关试题

