搜索
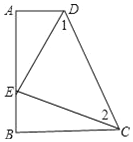
【题目】如图，∠A=∠B=90°，E是AB上的一点，且AE=BC，∠1=∠2．
求证：（1）△ADE≌△BEC
（2）△CDE是直角三角形．
参考答案：
【答案】（1）证明见解析（2）证明见解析
【解析】
（1）根据∠1=∠2，得DE=CE，利用“HL”可证明Rt△ADE≌Rt△BEC；
（2）是直角三角形，由Rt△ADE≌Rt△BEC得，∠3=∠4，从而得出∠4+∠5=90°，则△CDE是直角三角形．
（1）∵∠1=∠2，
∴DE=CE，
∵∠A=∠B=90°，
在Rt△ADE和Rt△BEC中，
∴Rt△ADE≌Rt△BEC（HL）；
（2）∵Rt△ADE≌Rt△BEC，
∴∠3=∠4，
∵∠3+∠5=90°，
∴∠4+∠5=90°，
∴∠DEC=90°，
∴△CDE是直角三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在△ABC中，AB=AC=2，∠A=90°，将一块与△ABC全等的三角板的直角顶点放在点C上，一直角边与BC重叠．
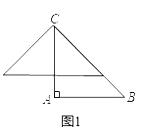
（1）操作1：固定△ABC，将三角板沿C→B方向平移，使其直角顶点落在BC的中点M，如图2所示，探究：三角板沿C→B方向平移的距离为；
（2）操作2：在（1）的情况下，将三角板BC的中点M顺时针方向旋转角度a（0°＜a＜90°），如图3所示，探究：设三角形板两直角边分别与AB、AC交于点P、Q，观察四边形MPAQ形状的变化，问：四边形MPAQ的面积S是否改变，若不变，求其面积；若改变，试说明理由；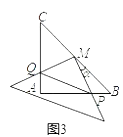
（3）在（2）的情形下，连PQ，则当△MPQ的面积等于四边形MPAQ的面积的一半时，四边形MPAQ的形状为 ， 此时BP= ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣
x2+bx+c与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．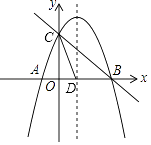
（1）求抛物线的解析式
（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，请直接写出P点的坐标；如果不存在，请说明理由．
（3）点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，△CBF的面积最大？请求出△CBF的最大面积及此时E点的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】为了提高学生书写汉字的能力．增强保护汉字的意识，我区举办了“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
组别
成绩x分
频数（人数）
第1组
25≤x＜30
4
第2组
30≤x＜35
6
第3组
35≤x＜40
14
第4组
40≤x＜45
a
第5组
45≤x＜50
10
请结合图表完成下列各题：
（1）求表中a的值；
（2）请把频数分布直方图补充完整；
（3）若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？
-
科目： 来源： 题型：
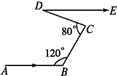
查看答案和解析>>【题目】某江段江水流经B,C,D三点拐弯后与原来流向相同,如图,若∠ABC=120°,∠BCD=80°,则∠EDC=___________°.
-
科目： 来源： 题型：
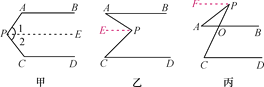
查看答案和解析>>【题目】阅读下列解答过程：（1）如图甲，AB∥CD，探索∠P与∠A，∠C之间的关系．
（2）如图乙和图丙，AB∥CD，请根据上述方法分别探索两图中∠P与∠A，∠C之间的关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：二次函数y=ax2+bx+c的图象所示，下列结论中：①abc＞0；②2a+b=0；③当m≠1时，a+b＞am2+bm；④a﹣b+c＞0；⑤若ax12+bx1=ax22+bx2 ， 且x1≠x2 ， 则x1+x2=2，正确的个数为（ ）
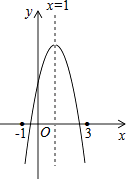
A.1个
B.2个
C.3个
D.4个
相关试题
