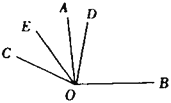
【题目】如图,已知同一平面内![]() ,
,![]() .
.
(1)问题发现:![]() 的余角是_____,
的余角是_____,![]() 的度数是_____;
的度数是_____;
(2)拓展探究:若![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,则
,则![]() 的度数是_____.
的度数是_____.
(3)类比延伸:在(2)的条件下,如果将题目中的![]() 改为
改为![]() ;
;![]() 改为
改为![]() ,其他条件不变,你能求出
,其他条件不变,你能求出![]() 吗?若能,请你写出求解过程;若不能,请说明理由.
吗?若能,请你写出求解过程;若不能,请说明理由.
参考答案:
【答案】(1)∠AOD,150°;(2)45°;(3)![]() =
=![]()
【解析】
(1)根据题意可得∠BOD+∠AOD=90°,即可得到![]() 的余角,根据
的余角,根据![]() ,
,![]() 即可求出
即可求出![]() ;
;
(2)由(1)的结论可求∠COD=75°,根据![]() 平分
平分![]() 可求∠COE=30°,由此可计算得出
可求∠COE=30°,由此可计算得出![]() 的度数;
的度数;
(3)先求出∠BOC=![]() ,类比(2)的方法求解即可.
,类比(2)的方法求解即可.
(1)∵![]() ,
,
∴∠BOD+∠AOD=90°,
∴![]() 的余角是∠AOD,
的余角是∠AOD,
∵![]() ,
,![]() ,
,
∴![]() =∠AOB+∠AOC=150°,
=∠AOB+∠AOC=150°,
故答案为:∠AOD,150°;
(2)由(1)知![]() =150°,
=150°,
∵![]() 平分
平分![]() ,
,
∴∠COD=75°,
∵![]() 平分
平分![]() ,
,
∴∠COE=30°,
∴![]() =∠COD-∠COE=45°,
=∠COD-∠COE=45°,
故答案为:45°;
(3)能求出![]() 的度数,
的度数,
∵![]() ,
,![]() ,
,
∴∠BOC=![]()
∵![]() 平分
平分![]() ,
,![]() ,
,
∴∠COD=![]() ,
,
∵![]() 平分
平分![]() ,
,![]()
∴∠COE=![]() ,
,
∴![]() =∠COD-∠COE=
=∠COD-∠COE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乐乐和数学小组的同学们研究了如下问题,请你也来试一下吧.
点
 是直线
是直线 上一点,在同一平面内,乐乐他们把一个等腰直角三角板
上一点,在同一平面内,乐乐他们把一个等腰直角三角板 任意放,其中直角顶点
任意放,其中直角顶点 与点
与点 重合,过点
重合,过点 作直线
作直线 ,垂足为点
,垂足为点 ,从过点
,从过点 作
作 ,垂足为点
,垂足为点 .
.(1)当直线
 ,
, 位于点
位于点 的异侧时,如图1,线段
的异侧时,如图1,线段 ,
, ,
, 之间的数量关系___(不必说明理由);
之间的数量关系___(不必说明理由);(2)当直线
 ,
, 位于点
位于点 的右侧时,如图2,判断线段
的右侧时,如图2,判断线段 ,
, ,
, 之间的数量系,并说明理由;
之间的数量系,并说明理由;(3)当直线
 ,
, 位于点
位于点 的左侧时,如图3,请你补全图形,并直接写出线段
的左侧时,如图3,请你补全图形,并直接写出线段 ,
, ,
, 之间的数量关系.
之间的数量关系.


-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程交由甲、乙两个工程队来完成,已知甲工程队单独完成需要60天,乙工程队单独完成需要40天
(1)若甲工程队先做30天后,剩余由乙工程队来完成,还需要用时 天
(2)若甲工程队先做20天,乙工程队再参加,两个工程队一起来完成剩余的工程,求共需多少天完成该工程任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用“※”定义一种新运算:对于任意有理数a和b,规定a※b=ab2+2ab+a.
如:1※2=1×22+2×1×2+1=9
(1)(﹣2)※3= ;
(2)若
 ※3=16,求a的值;
※3=16,求a的值;(3)若2※x=m,(
 x)※3=n(其中x为有理数),试比较m,n的大小.
x)※3=n(其中x为有理数),试比较m,n的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5
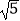 cm,且tan∠EFC=0.75,则矩形ABCD的周长为 .
cm,且tan∠EFC=0.75,则矩形ABCD的周长为 . 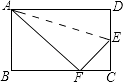
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用网格画图:
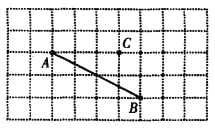
(1)过点C画AB的平行线CD;
(2)过点C画AB的垂线,垂足为E;
(3)线段CE的长度是点C到直线_______的距离;
(4)连接CA、CB,在线段CA、CB、CE中,线段_______最短,理由:_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,DE分别是AB,AC上的点,且AD=CE.
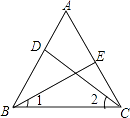
(1)求证:BE=CD;
(2)求∠1+∠2的度数.
相关试题

