【题目】如图,在等边△ABC中,DE分别是AB,AC上的点,且AD=CE.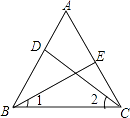
(1)求证:BE=CD;
(2)求∠1+∠2的度数.
参考答案:
【答案】
(1)证明:∵△ABC是等边三角形,
∴∠A=∠ACB=60°,AC=BC,
在△ACD和△CBE中
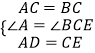
∴△ACD≌△CBE(SAS),
∴BE=CD;
(2)解:∵△ACD≌△CBE,
∴∠1=∠ACD,
∴∠1+∠2=∠ACD+∠2=∠ACB=60°.
【解析】(1)首先根据等边三角形的性质可得到∠A=∠ACB=60°,AC=BC,然后,再利用SAS证明△ACD≌△CBE,最后,依据全等三角形对应边相等进行证明即可;
(2)依据全等三角形对应角相等可得到 ∠1=∠ACD,通过等量代换可得到∠1+∠2=∠ACB,故此可得到问题的答案.
【考点精析】掌握等边三角形的性质是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知同一平面内
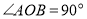 ,
,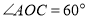 .
.(1)问题发现:
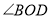 的余角是_____,
的余角是_____,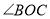 的度数是_____;
的度数是_____;(2)拓展探究:若
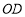 平分
平分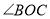 ,
,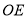 平分
平分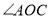 ,则
,则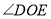 的度数是_____.
的度数是_____.(3)类比延伸:在(2)的条件下,如果将题目中的
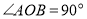 改为
改为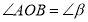 ;
;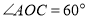 改为
改为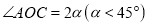 ,其他条件不变,你能求出
,其他条件不变,你能求出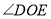 吗?若能,请你写出求解过程;若不能,请说明理由.
吗?若能,请你写出求解过程;若不能,请说明理由.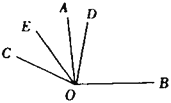
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5
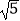 cm,且tan∠EFC=0.75,则矩形ABCD的周长为 .
cm,且tan∠EFC=0.75,则矩形ABCD的周长为 . 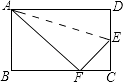
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用网格画图:
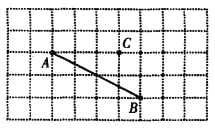
(1)过点C画AB的平行线CD;
(2)过点C画AB的垂线,垂足为E;
(3)线段CE的长度是点C到直线_______的距离;
(4)连接CA、CB,在线段CA、CB、CE中,线段_______最短,理由:_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:
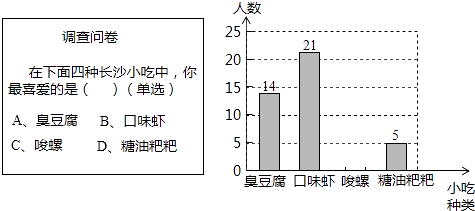
请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?
(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图甲,AB∥CD,试问∠2与∠1+∠3的关系是什么,为什么?
(2)如图乙,AB∥CD,试问∠2+∠4与∠1+∠3+∠5一样大吗?为什么?
(3)如图丙,AB∥CD,试问∠2+∠4+∠6与∠1+∠3+∠5+∠7哪个大?为什么?
你能将它们推广到一般情况吗?请写出你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)某中学初二年级抽取部分学生进行跳绳测试.并规定:每分钟跳90次以下的为不及格;每分钟跳90~99次的为及格;每分钟跳100~109次的为中等;每分钟跳110~119次的为良好;每分钟跳120次及以上的为优秀.测试结果整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:

(1)参加这次跳绳测试的共有 人;
(2)补全条形统计图;
(3)在扇形统计图中,“中等”部分所对应的圆心角的度数是 ;
(4)如果该校初二年级的总人数是480人,根据此统计数据,请你估算该校初二年级跳绳成绩为“优秀”的人数.
相关试题

